
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.
调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列表,并判断是否由
列表,并判断是否由![]() 的把握认为.了解阿基米德与选择文理科有关?
的把握认为.了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | p> | ||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取两人,求两人都是文科生的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
【答案】(1)见解析;(2)(i)文科生3人,理科生7人 (ii)![]()
【解析】
(1)依题意填写![]() 列联表,根据公式,求得
列联表,根据公式,求得![]() 的值,即可得到结论.
的值,即可得到结论.
(2)(i)按照文理科采用分层抽样的方法,即可得到文科生人数是![]() 人,理科生人数是
人,理科生人数是![]() 人.
人.
(ii)记“两人都是文科生”为事件![]() ,记样本中的3名文科生为
,记样本中的3名文科生为![]() ,7名理科生为
,7名理科生为![]() 从10人的样本中随机抽取两人,利用列举法求得基本事件的总数,利用古典概型的概率公式,即可求解.
从10人的样本中随机抽取两人,利用列举法求得基本事件的总数,利用古典概型的概率公式,即可求解.
(1)依题意填写![]() 的列联表如下:
的列联表如下:
比较了解 | 不太了解 | 合计 | |
理科生 | 42 | 28 | 70 |
文科生 | 12 | 18 | 30 |
合计 | 54 | 46 | 100 |
计算![]() ,
,
![]() 没有
没有![]() 的把握认为,了解阿基米德与选择文理科有关.
的把握认为,了解阿基米德与选择文理科有关.
(2)(i)抽取的文科生人数是![]() (人),理科生人数是
(人),理科生人数是![]() (人).
(人).
(ii)记“两人都是文科生”为事件![]() ,记样本中的3名文科生为
,记样本中的3名文科生为![]() ,7名理科生为
,7名理科生为![]() 从10人的样本中随机抽取两人,则所有的基本事件有:
从10人的样本中随机抽取两人,则所有的基本事件有:
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() ,共45种,
,共45种,
两人都是文科生的基本事件有:![]() ,共3种,
,共3种,
故由古典概型得,两人都是文科生的概率是![]() .
.


科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天津市某学校组织教师进行“学习强国”知识竞赛,规则为:每位参赛教师都要回答3个问题,且对这三个问题回答正确与否相互之间互不影响,若每答对1个问题,得1分;答错,得0分,最后按照得分多少排出名次,并分一、二、三等奖分别给予奖励.已知对给出的3个问题,教师甲答对的概率分别为![]() ,
,![]() ,p.若教师甲恰好答对3个问题的概率是
,p.若教师甲恰好答对3个问题的概率是![]() ,则
,则![]() ________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求证:当x∈(0,π]时,f(x)<1;
(2)求证:当m>2时,对任意x0∈(0,π] ,存在x1∈(0,π]和x2∈(0,π](x1≠x2)使g(x1)=g(x2)=f(x0)成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,若a=5![]() sin(B
sin(B![]() ),c=5且O为△ABC的外心,G为△ABC的重心,则OG的最小值为( )
),c=5且O为△ABC的外心,G为△ABC的重心,则OG的最小值为( )
A.![]() 1B.
1B.![]() C.
C.![]() 1D.
1D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对于函数![]() 定义域内任意的两个自变量的值
定义域内任意的两个自变量的值![]() ,
,![]() ,当
,当![]() 时,都有
时,都有![]() ,且存在两个不相等的自变量值
,且存在两个不相等的自变量值![]() ,
,![]() ,使得
,使得![]() ,就称
,就称![]() 为定义域上的“不严格的增函数”.下列所给的四个函数中为“不严格增函数”的是( )
为定义域上的“不严格的增函数”.下列所给的四个函数中为“不严格增函数”的是( )
A.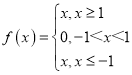 ;B.
;B.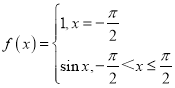 ;
;
C.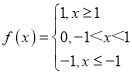 ;D.
;D.![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com