
【题目】已知命题p:x∈[1,2],x2≥a;命题q:x∈R,x2+2ax+2﹣a=0,若命题p∧q是真命题,则实数a的取值范围是( )
A.a≤﹣2或a=1
B.a≤﹣2或1≤a≤2
C.a≥1
D.﹣2≤a≤1
科目:高中数学 来源: 题型:
【题目】已知a1=3,an=2an﹣1+(t+1)2n+3m+t(t,m∈R,n≥2,n∈N*)
(1)t=0,m=0时,求证: ![]() 是等差数列;
是等差数列;
(2)t=﹣1,m= ![]() 是等比数列;
是等比数列;
(3)t=0,m=1时,求数列{an}的通项公式和前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间四边形ABCD的两条对角线的长AC=6,BD=8,AC与BD所成的角为30o , E,F,G,H分别是AB,BC,CD,DA的中点,求四边形EFGH的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有老年人30人,中年人90人,青年人60人,为了调查他们的身体健康状况,采用分层抽样的方法从他们中间抽取一个容量为36的样本,则应抽取老年人的人数是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,
, ![]() 为椭圆的半焦距,且
为椭圆的半焦距,且![]() ,过点
,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别交于另两点
分别交于另两点![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的面积;
的面积;
(3)若线段![]() 的中点在
的中点在![]() 轴上,求直线
轴上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
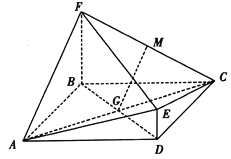
【题目】如图,菱![]() 与四边形BDEF相交于BD,
与四边形BDEF相交于BD, ![]() 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M为CF的中点, ![]() .
.
(I)求证:GM//平面CDE;
(II)求证:平面ACE⊥平面ACF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com