
【题目】用一个半径为12厘米圆心角为![]() 的扇形纸片PAD卷成一个侧面积最大的无底圆锥(接口不用考虑损失),放于水平面上.
的扇形纸片PAD卷成一个侧面积最大的无底圆锥(接口不用考虑损失),放于水平面上.
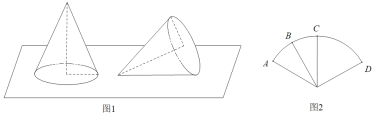
(1)无底圆锥被一阵风吹倒后(如图1),求它的最高点到水平面的距离;
(2)扇形纸片PAD上(如图2),C是弧AD的中点,B是弧AC的中点,卷成无底圆锥后,求异面直线PA与BC所成角的大小.
科目:高中数学 来源: 题型:
【题目】设函数![]() 、
、![]() 的定义域均为
的定义域均为![]() ,若对任意
,若对任意![]() ,且
,且![]() ,具有
,具有![]() ,则称函数
,则称函数![]() 为
为![]() 上的单调非减函数,给出以下命题:① 若
上的单调非减函数,给出以下命题:① 若![]() 关于点
关于点![]() 和直线
和直线![]() (
(![]() )对称,则
)对称,则![]() 为周期函数,且
为周期函数,且![]() 是
是![]() 的一个周期;② 若
的一个周期;② 若![]() 是周期函数,且关于直线
是周期函数,且关于直线![]() 对称,则
对称,则![]() 必关于无穷多条直线对称;③ 若
必关于无穷多条直线对称;③ 若![]() 是单调非减函数,且关于无穷多个点中心对称,则
是单调非减函数,且关于无穷多个点中心对称,则![]() 的图象是一条直线;④ 若
的图象是一条直线;④ 若![]() 是单调非减函数,且关于无穷多条平行于
是单调非减函数,且关于无穷多条平行于![]() 轴的直线对称,则
轴的直线对称,则![]() 是常值函数;以上命题中,所有真命题的序号是_________
是常值函数;以上命题中,所有真命题的序号是_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左.右焦点分别为
的左.右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 的边长为
的边长为![]() 的正方形.
的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若![]() ,分别是椭圆长轴的左,右端点,动点
,分别是椭圆长轴的左,右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() .证明:
.证明: ![]() 的定值;
的定值;
(Ⅲ)在(Ⅱ)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() ,的定点
,的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求直线![]() 及曲线
及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() (与原点不重合),求
(与原点不重合),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立直角坐标系.过点
轴建立直角坐标系.过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程,并写出直线
的直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)过点![]() 的另一条直线
的另一条直线![]() 与
与![]() 关于直线
关于直线![]() 对称,且与曲线
对称,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院为筛查某种疾病,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:①逐份检验,列需要检验
份血液样本,有以下两种检验方式:①逐份检验,列需要检验![]() 次;②混合检验,将其
次;②混合检验,将其![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验.若检验结果为阴性,这
)份血液样本分别取样混合在一起检验.若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验的方式,求恰好经过3次检验就能把阳性样本全部检验出来的概率.
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(ii)若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点在椭圆
的对称点在椭圆![]() 上.
上.
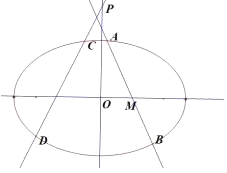
(1)求椭圆![]() 的方程;
的方程;
(2)如图,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() (点
(点![]() 在点
在点![]() 的上方),试求
的上方),试求![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,是否存在直线
,是否存在直线![]() (其中
(其中![]() ),使得
),使得![]() 到直线
到直线![]() 的距离
的距离![]() 满足
满足![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com