
【题目】如图,在棱台ABC﹣FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点, ![]() .
. 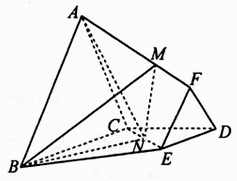
(Ⅰ)λ为何值时,MN∥平面ABC?
(Ⅱ)在(Ⅰ)的条件下,求直线AN与平面BMN所成角的正弦值.
【答案】解:(Ⅰ)当 ![]() ,即M为AF中点时MN∥平面ABC. 事实上,取CD中点P,连接PM,PN,
,即M为AF中点时MN∥平面ABC. 事实上,取CD中点P,连接PM,PN,
∵AM=MF,CP=PD,∴MP∥AC,
∵AC平面ABC,MP平面ABC,∴MP∥平面ABC.
由CP∥PD,CN∥NE,得NP∥DE,
又DE∥BC,∴NP∥BC,
∵BC平面ABC,NP平面ABC,∴NP∥平面ABC.
∴平面MNP∥平面ABC,则MN∥平面ABC;
(Ⅱ)取BC中点O,连OA,OE,
∵AB=AC,OB=OC,∴AO⊥BC,
∵平面ABC⊥平面BCDE,且AO平面ABC,∴AO⊥平面BCDE,
∵OC= ![]() ,BC∥ED,∴OE∥CD,
,BC∥ED,∴OE∥CD,
又CD⊥BC,∴OE⊥BC.
分别以OE,OC,OA所在直线为x轴,y轴,z轴,建立空间直角坐标系.
则A(0,0, ![]() ),C(0,1,0),E(1,0,0),
),C(0,1,0),E(1,0,0),  ,
,
∴F(1, ![]() ,
, ![]() ),M(
),M( ![]() ,
, ![]() ,
, ![]() ),N(
),N( ![]() ).
).
设 ![]() 为平面BMN的法向量,则
为平面BMN的法向量,则 ,取z=1,得
,取z=1,得 ![]() .
.
cos< ![]() >=
>= ![]() .
.
∴直线AN与平面MNB所成角的正弦值为 ![]() .
.
【解析】 (Ⅰ)取CD中点P,连接PM,PN,可得MP∥AC,则MP∥平面ABC.再由已知证明NP∥平面ABC.得到平面MNP∥平面ABC,则MN∥平面ABC;(Ⅱ)取BC中点O,连OA,OE,可证AO⊥BC,OE⊥BC.分别以OE,OC,OA所在直线为x轴,y轴,z轴,建立空间直角坐标系.求出所用点的坐标,得到平面BMN的法向量,求出< ![]() >的余弦值,即可得到直线AN与平面MNB所成角的正弦值.
>的余弦值,即可得到直线AN与平面MNB所成角的正弦值.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】某同学在研究函数![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①函数f(x)是奇函数;②函数f(x)的值域为(-1,1);③函数f(x)在R上是增函数;其中正确结论的序号是
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]()
(1)求证:直线![]() 过定点;
过定点;
(2)求直线![]() 被圆
被圆![]() 所截得的弦长最短时
所截得的弦长最短时![]() 的值;
的值;
(3)已知点![]() ,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有
,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点N的坐标及该常数.
为一常数,试求所有满足条件的点N的坐标及该常数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,若曲线
,若曲线 ![]() 上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
A.[0,e2﹣e+1]
B.[0,e2+e﹣1]
C.[0,e2+e+1]
D.[0,e2﹣e﹣1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .点
.点![]() 为圆
为圆![]() 上任意一点,
上任意一点, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 相切,
相切, ![]() 与圆
与圆![]() 相交于另一点
相交于另一点![]() ,点
,点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,证明:直线
,证明:直线![]() 与椭圆
与椭圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
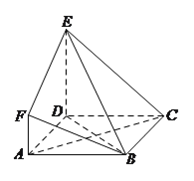
【题目】如图,![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)设点![]() 是线段
是线段![]() 上一个动点,试确定点
上一个动点,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com