考点:多面体和旋转体表面上的最短距离问题,棱柱、棱锥、棱台的体积,球的体积和表面积
专题:空间位置关系与距离
分析:(1)根据V
2对应的几何体为空间中与点A距离不大于
的所有点构造的几何体,即一个
球,求出体积后,进而求出V
1,可得
值;
(2)在正方体表面上与点A的距离为
的点形成的曲线是六段圆弧,分别求出其长度后,相加可得答案.
解答:
解:(1)根据V
2对应的几何体为空间中与点A距离不大于
的所有点构造的几何体,
即一个
球,
该球的半径为:
,
∴
V2=×π×()3=,
∴
V1=1-,
则
==.
(2)由题意:以A球心,
为半径的球面与正方体AC
1各侧面的截交线均为圆弧段.
球面与侧面AC、AB
1、AD
1所截得的圆弧段,如下图所示:
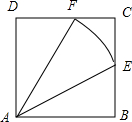
由AE=
,AB=1,则cos∠EAB=
,则∠EAB=
,进而∠EAF=
,
故这三段弧可视作均以A为圆心,圆心角均为
,半径均为
的圆弧,
从而相应圆弧段长为
×=π;
球面与侧面C
1A
1、C
1B、C
1D所截得的圆弧段,
可视作分别以A
1、B、D为圆心,圆心角均为
,
半径均为
=
的圆弧,
从而相应圆弧段长为
×=π;
从而球面与整个正方体相相截所得的空间区间长为
3×(π+π)=π.
点评:本题考查的知识点是球的体积,弧长公式,正方体的几何特征,球的几何特征,要求有较强的空间想像能力及运算能力,属于难题.

 已知正方体ABCD-A1B1C1D1的棱长为1.
已知正方体ABCD-A1B1C1D1的棱长为1.

