对称轴为坐标轴,顶点在坐标原点的抛物线C经过两点A(a,2a)、B(4a,4a),(其中a为正常数).
(1)求抛物线C的方程;
(2)设动点T(m,0)(m>a),直线AT、BT与抛物线C的另一个交点分别为A1、B1,当m变化时,记所有直线A1B1组成的集合为M,求证:集合M中的任意两条直线都相交且交点都不在坐标轴上.
【答案】
分析:(1)由于两点在第一象限内,故抛物线开口向右或向上,由此分两种情况利用待定系数法求得抛物线的标准方程;
(2)先将点A
1、B
1的坐标用a、m表示,再利用点斜式写出直线A
1B
1的方程,证明其斜率随m的变化而单调变化,即可证明集合M中的任意两条直线都相交,证明直线的截距不为零即可证明交点都不在坐标轴上.
解答:解:(1)当抛物线焦点在x轴上时,设抛物线方程y
2=2Px,
∵
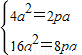
∴P=2a
∴y
2=4ax
当抛物线焦点在y轴上时,设抛物线方程x
2=2py
∵
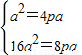
∴方程无解,抛物线不存在
∴抛物线C的方程y
2=4ax
(2)设A
1(as
2,2as)、B
1(at
2,2at) T(m,0)(m>a)
∵k
TA=k
TA1 ∴
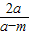
=
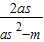
∴as
2+(m-a)s-m=0
∵(as+m)(s-1)=0∴S=-
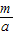
∴A
1(
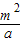
,-2m)
∵k
TB=k
TB1 ∴
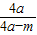
=
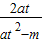
∵2at
2+(m-4a)t-2m=0∴(2at+m)(t-2)=0
∴t=-
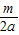
∴B
1(
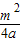
,-m)
∴l
A1B1的直线方程为y+2m=
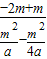
(x-
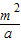
)
∵直线的斜率为f(m)=-
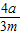
在m∈(a,+∞)单调
∴所以集合M中的直线必定相交,
∵直线的横截距为-
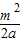
≠0,纵截距为-
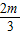
≠0
∴任意两条直线都相交且交点都不在坐标轴上.
点评:本题主要考查了抛物线的标准方程,待定系数法求曲线方程,直线方程,直线与抛物线的位置关系,直线相交的意义等知识,属中档题

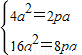 ∴P=2a
∴P=2a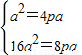 ∴方程无解,抛物线不存在
∴方程无解,抛物线不存在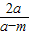 =
=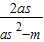
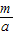
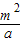 ,-2m)
,-2m) 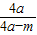 =
=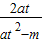
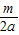 ∴B1(
∴B1(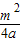 ,-m)
,-m) 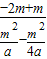 (x-
(x-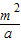 )
)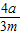 在m∈(a,+∞)单调
在m∈(a,+∞)单调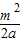 ≠0,纵截距为-
≠0,纵截距为-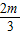 ≠0
≠0

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案