|
|
|
在数列{xn}中,a1=1, ,猜想这个数列的一个通项公式为 ,猜想这个数列的一个通项公式为
|
| [ ] |
A. |
an=n
|
B. |
an=2n-1
|
C. |
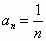
|
D. |
an=n2
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
在R上定义运算 :x :x y=x(1-y),要使不等式(x-a) y=x(1-y),要使不等式(x-a) (x+a)>1成立,则实数a的取值范围是 (x+a)>1成立,则实数a的取值范围是
|
| [ ] |
A. |
-1<a<1
|
B. |
0<a<2
|
C. |
a<- 或a> 或a>
|
D. |
- <a< <a<
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
已知函数f(x)=ln(x-1)+ (a∈R). (a∈R).
(1)若a=2时,试证明:当x≥2时,f(x)≥1;
(2)如果函数y=f(x)是定义域上的增函数,求a的取值范围;
(3)求证:ln(n+1)> + +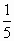 + + +…+ +…+ (n∈N*). (n∈N*).
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
函数f(x)的导函数为 (x),对任意的x∈R都有2 (x),对任意的x∈R都有2 (x)>f(x)成立,则 (x)>f(x)成立,则
|
| [ ] |
A. |
3f(2ln2)>2f(2ln3)
|
B. |
3f(2ln2)<2f(2ln3)
|
C. |
3f(2ln2)=2f(2ln3)
|
D. |
3f(2ln2)与2f(2ln3)的大小不确定
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
已知函数f(x)=2x2-4x+4+xlnx+8 m,m为实数.
(Ⅰ)证明:当x∈[1,+∞)时,f(x)≥(x-1)lnx+x+8 m+1恒成立;
(Ⅱ)当x>2时,f(x)>4 mx恒成立,求整数m的最大值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
函数 在x等于________处取得极值. 在x等于________处取得极值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
等比数列{an}中,已知对任意正自然数n,a1+a2+a3+…+an=2n-1,则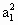 + + + + +…+a +…+a 等于 等于
|
| [ ] |
A. |
(2n-1)2
|
B. |
 (2n-1) (2n-1)
|
C. |
4n-1
|
D. |
 (4n-1) (4n-1)
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 选修1-1
题型:
|
|
|
已知双曲线 的实轴在y轴上且焦距为8,则双曲线的渐近线的方程为 的实轴在y轴上且焦距为8,则双曲线的渐近线的方程为
|
| [ ] |
A. |
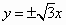
|
B. |
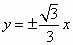
|
C. |
y=±3x
|
D. |
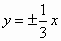
|
|
|
查看答案和解析>>

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案