
【题目】已知三棱锥![]() 的展开图如图二,其中四边形
的展开图如图二,其中四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
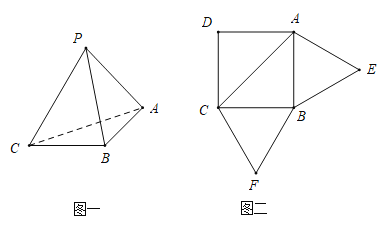
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,由边长关系得
,由边长关系得![]() ,从而可得
,从而可得![]() 平面
平面![]() ,即可证明平面
,即可证明平面![]() 平面
平面![]() ;
;
(2)由(1)问可知![]() 平面
平面![]() ,所以以
,所以以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图示空间直角坐标系,利用向量法求出平面
轴建立如图示空间直角坐标系,利用向量法求出平面![]() 和平面
和平面![]() 的法向量,再利用二面角的公式即可得到二面角
的法向量,再利用二面角的公式即可得到二面角![]() 的余弦值。
的余弦值。
(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,
,
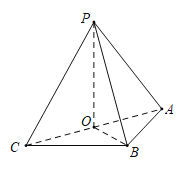
由题意,得![]() ,
,![]() ,
,![]() .
.
因为在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
因为在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,所以
,所以![]()
因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(2)由(1)问可知![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,于是以
,于是以![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图示空间直角坐标系,
轴建立如图示空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由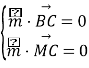 得:
得: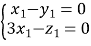 .令
.令![]() ,得
,得![]() ,
,![]() ,即
,即
![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由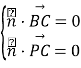 得:
得:
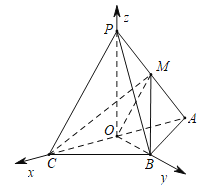
 ,令
,令![]() ,得
,得![]() ,
,![]() ,即
,即![]()
 .由图可知,二面角
.由图可知,二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】现有0、1、2、3、4、5、6、7、8、9共十个数字.
(1)可以组成多少个无重复数字的三位数?
(2)组成无重复数字的三位数中,315是从小到大排列的第几个数?
(3)可以组成多少个无重复数字的四位偶数?
(4)选出一个偶数和三个奇数,组成无重复数字的四位数,这样的四位数共有多少个?
(5)如果一个数各个数位上的数字从左到右按由大到小的顺序排列,则称此正整数为“渐减数”, 那么由这十个数字组成的所有“渐减数”共有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了100名用户,得到用户的满意度评分(满分10分),现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
频数 | 5 | 10 | a | 32 | 16 |
频率 | 0.05 | b | 0.37 | c | 0.16 |
(1)求表格中的a,b,c的值;
(2)估计用户的满意度评分的平均数;
(3)若从这100名用户中随机抽取25人,估计满意度评分低于6分的人数为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
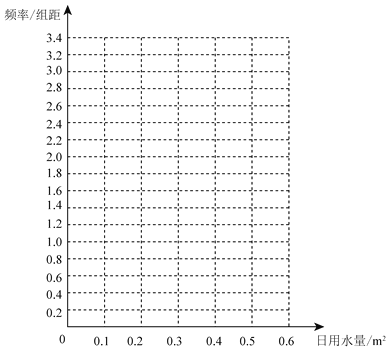
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数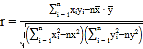 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: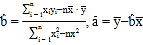 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,圆C的直角坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),射线OM的极坐标方程为
(t为参数),射线OM的极坐标方程为![]() .
.
(1)求圆C和直线l的极坐标方程;
(2)已知射线OM与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com