练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
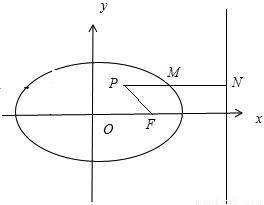
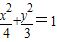    椭圆内有一点P（1，1），F为右焦点，椭圆上的点M使得MP+2MF的值最小，则点M的坐标为    ．
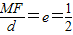    【答案】分析：由椭圆的第二定义可知， 可得d=2MF，从而有|PM|+2|MF|=d+|PM|由题意可得，过P作PN⊥l，当M为该垂线与椭圆的右交点时，所求的值最小．
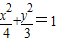    解答：解：∵椭圆的a=2，b=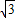，c=1，e=．
    由题意可得点P在椭圆内部，设M到椭圆的左准线l得距离为d
    由椭圆的第二定义可知，，
    ∴d=2MF，
    ∴|PM|+2|MF|=d+|PM|
    由题意可得，过P作PN⊥l，当M为该垂线与椭圆的右交点时，所求的值最小，
    此时 yM=1，代入可得
    故答案为：．
    点评：本题主要考查了椭圆的第二定义的应用，解题得关键是灵活利用定义转化可得|PM|+2|MF|=d+|PM|，从而结合图象可求，体现了数形结合的思想的应用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

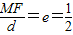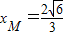
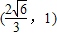    科目：高中数学 来源：2012年苏教版高中数学选修1-1 2.2椭圆练习卷（解析版） 题型：选择题

    在椭圆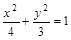内有一点P（1，－1），F为椭圆右焦点，在椭圆上有一点M，使|MP|+2|MF|的值最小，则这一最小值是    （    ）

    A．                 B．             C．3              D．4

     

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学选修1-1 2.1椭圆练习卷（解析版） 题型：选择题

    在椭圆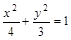内有一点P（1，－1），F为椭圆右焦点，在椭圆上有一点M，使|MP|+2|MF|的值最小，则这一最小值是                       （    ）

    A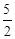．                 B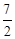．             C．3              D．4

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江西省南昌市四校高二（上）第二次联考数学试卷（理科）（解析版） 题型：填空题

    在椭圆内有一点P（1，-1），F为椭圆右焦点，在椭圆上有一点M，使|MP|+2|MF|的值最小，则M的坐标    ．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年重庆市第二外国语学校高二（上）期中数学试卷（理科）（解析版） 题型：解答题

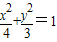    已知椭圆内有一点P（1，-1），F是椭圆的右焦点．
    （1）求该椭圆的离心率．
    （2）在椭圆上求一点M，使得|MP|+2|MF|的值最小，并求出这个最小值．

    查看答案和解析>>

    同步练习册答案