练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数y＝f（x）的定义域为D，若对任意的x1∈D，总存在x2∈D，使得f（x1）f（x2）＝1，则称函数f（x）具有性质M.下列结论：①函数y＝x3﹣x具有性质M；②函数y＝3x+5x具有性质M；③若函数y＝log8（x+2），x∈[0，t]时具有性质M，则t＝510；④若y具有性质M，则a＝5.其中正确结论的序号是_____.

    【答案】②③.

    【解析】

    对于①，当时，不存在满足；

    对于②，由于，所以具有性质；

    对于③，由于时，，所以时必有，所以；

    对于④，由于，所以可得.

    对于①，当时，不存在满足，故①不正确；

    对于②，由于，所以，所以具有性质，故②正确；

    对于③，由于为增函数，且时，，所以时必有，所以，故③正确；

    对于④，由于，若y具有性质M，所以可得，故④不正确.

    故答案为：②③.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】“绿水青山就是金山银山”，“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容，某班在一次研学旅行活动中，为了解某苗圃基地的柏树幼苗生长情况，在这些树苗中随机抽取了120株测量高度（单位：），经统计，树苗的高度均在区间内，将其按，，，，，分成6组，制成如图所示的频率分布直方图.据当地柏树苗生长规律，高度不低于的为优质树苗.

    (1)求图中的值；

    (2)已知所抽取的这120株树苗来自于，两个试验区，部分数据如下列联表：

    试验区

    试验区

    合计

    优质树苗

    20

    非优质树苗

    60

    合计

    将列联表补充完整，并判断是否有99.9%的把握认为优质树苗与，两个试验区有关系，并说明理由；

    (3)通过用分层抽样方法从试验区被选中的树苗中抽取5株，若从这5株树苗中随机抽取2株，求优质树苗和非优质树苗各有1株的概率.

    附：参考公式与参考数据：

    其中

    0.010

    0.005

    0.001

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为平行四边形，平面，.

    （1）证明：平面；

    （2）若与平面所成角为45°，求二面角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为美化校园，江苏省淮阴中学将一个半圆形的边角地改造为花园.如图所示，O为圆心，半径为1千米，点A、B、P都在半圆弧上，设∠NOP=∠POA=，∠AOB=，且.

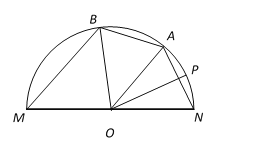
    （1）请用分别表示线段NA、BM的长度；

    （2）若在花园内铺设一条参观线路，由线段NA、AB、BM三部分组成，则当取何值时，参观线路最长？

    （3）若在花园内的扇形ONP和四边形OMBA内种满杜鹃花，则当取何值时，杜鹃花的种植总面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市2010年4月1日—4月30日对空气污染指数的监测数据如（主要污染物为可吸入颗粒物）：61，76，70，56，81，91，92，91，75，81，88，67，101，103，95，91，77，86，83，82，82，64，79，86，85，75，71，49，45．

    样本频率分布表：

    分组

    频数

    频率

    [41，51）

    2

    [51，61）

    1

    [61，71）

    4

    [71，81）

    6

    [81，91）

    10

    [91，101）

    [101，111）

    2

    （1） 完成频率分布表；

    （2）作出频率分布直方图；

    （3）根据国家标准，污染指数在0~50之间时，空气质量为优：在51~100之间时，为良；在101~150之间时，为轻微污染；在151~200之间时，为轻度污染．请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于数列{an}，若从第二项起的每一项均大于该项之前的所有项的和，则称{an}为P数列.

    （1）若{an}的前n项和Sn＝3n+2，试判断{an}是否是P数列，并说明理由；

    （2）设数列a1，a2，a3，…，a10是首项为﹣1、公差为d的等差数列，若该数列是P数列，求d的取值范围；

    （3）设无穷数列{an}是首项为a、公比为q的等比数列，有穷数列{bn}，{cn}是从{an}中取出部分项按原来的顺序所组成的不同数列，其所有项和分别为T1，T2，求{an}是P数列时a与q所满足的条件，并证明命题“若a＞0且T1＝T2，则{an}不是P数列”.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】由我国引领的5G时代已经到来，5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展，进而对增长产生直接贡献，并通过产业间的关联效应和波及效应，间接带动国民经济各行业的发展，创造岀更多的经济增加值.如图是某单位结合近年数据，对今后几年的5G经济产出所做的预测.结合下图，下列说法正确的是（ ）

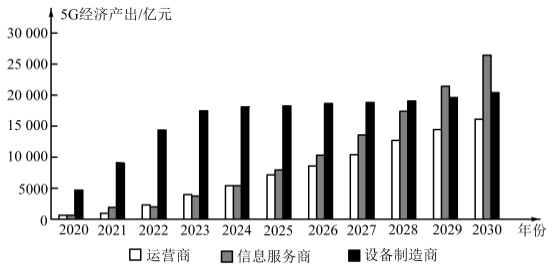
    A.5G的发展带动今后几年的总经济产出逐年增加

    B.设备制造商的经济产出前期增长较快，后期放缓

    C.设备制造商在各年的总经济产出中一直处于领先地位

    D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在矩形中，，为边的中点，以为折痕把折起，使点到达点的位置，且使平面平面.

    （1）证明：平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对由和这两个数字组成的字符串,作如下规定:按从左向右的顺序,当第一个子串“”的最后一个所在数位是第(,且)位,则称子串“”在第位出现;再继续从第位按从左往右的顺序找子串“”,若第二个子串“”的最后一个所在数位是第位(其中且),则称子串“”在第位出现;……;如此不断地重复下去.如:在字符串中,子串“”在第位和第位出现,而不是在第位和第位出现.记在位由组成的所有字符串中,子串“”在第位出现的字符串的个数为.

    （1）求的值;

    （2）求证:对任意的正整数,是的倍数.

    查看答案和解析>>

    同步练习册答案