
设f(x)=x2+px+q,A={x|x=f(x)},B={x|f[f(x)]=x}.
(1)求证:A![]() B;
B;
(2)如果A={-1,3},求B
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:江苏省南通市海门市2008届高三第一次诊断性考试数学(文) 题型:044
设命题p:函数![]() 是R上的减函数,命题q:函数f(x)=x2-4x+3在[0,a]的值域为[-1,3].若“p且q”为假命题,“p或q”为真命题,求a的取值范围.
是R上的减函数,命题q:函数f(x)=x2-4x+3在[0,a]的值域为[-1,3].若“p且q”为假命题,“p或q”为真命题,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试、文科数学(湖北卷) 题型:044
设函数f(x)=![]() x2-
x2-![]() x2+bx+c,其中a>0.曲线y=f(x)在点p(0,f(0))处的切线方程为y=1.
x2+bx+c,其中a>0.曲线y=f(x)在点p(0,f(0))处的切线方程为y=1.
(1)确定b,c的值
(2)设曲线y=f(x)在点(x1,f(x1))及(x2,f(x2))处的切线都过点(0,2).证明:当x1≠x2时,![]() (x1)≠
(x1)≠![]() (x2);
(x2);
(3)若过点(0,2)可作曲线y=f(x)的三条不同切线,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:浙江慈溪市2012届高三5月模拟考试数学理科试题 题型:044
已知函数f(x)=x2-(a+2)x+alnx.(1)当a=1时,求函数f(x)的极值;(2)设定义在D上的函数y=g(x)在点P(x0,y0)处的切线方程为l:y=h(x),当x≠x0时,若![]() 在D内恒成立,则称P为函数y=g(x)的“Hold点”.当a=4时,试问函数y=f(x)是否存在“Hold点”,若存在,请求出“Hold点”的横坐标,若不存在,请说明理由.
在D内恒成立,则称P为函数y=g(x)的“Hold点”.当a=4时,试问函数y=f(x)是否存在“Hold点”,若存在,请求出“Hold点”的横坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届四川省成都外国语学校高二下学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)设命题p:函数 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在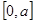 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期第二次月考文科数学试卷 题型:解答题
设命题p:函数 是R上的减函数,
是R上的减函数,
命题q:函数f(x)=x2-4x+3在 上的值域为[-1,3],
上的值域为[-1,3],
若“p且q”为假命题,“p或q”为真命题,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com