
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,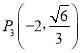 ,
,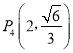 中恰有三个点在椭圆C上,左、右焦点分别为F1、F2.
中恰有三个点在椭圆C上,左、右焦点分别为F1、F2.
(1)求椭圆C的方程;
(2)过左焦点F1且不平行坐标轴的直线l交椭圆于P、Q两点,若PQ的中点为N,O为原点,直线ON交直线x=﹣3于点M,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由椭圆的对称性可得P2,P3,P4在椭圆上,进而求出椭圆的方程;
(2)由(1)可得F1的坐标,由题意设直线l的方程与椭圆联立,求出两根之和及两根之积,求出PQ的中点N的坐标,再由直线ON与x=﹣3,求出M的坐标,进而求出![]() 的表达式,换元由二次函数配方可得其最大值.
的表达式,换元由二次函数配方可得其最大值.
解:(1)由椭圆的对称性易知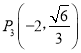 ,
,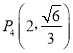 关于y轴对称,
关于y轴对称,
一定都在椭圆上.所以![]() 一定不在椭圆上.
一定不在椭圆上.
根据题意![]() 也在椭圆上,
也在椭圆上,
将![]() ,
,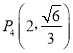 带入椭圆方程,解得椭圆方程为
带入椭圆方程,解得椭圆方程为![]() ;
;
(2)设直线l方程为y=k(x+2)(k≠0),P(x1,y1),Q(x2,y2),
联立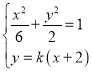 ,可得(3k2+1)x2+12k2x+12k2﹣6=0;
,可得(3k2+1)x2+12k2x+12k2﹣6=0;
则![]() =24(k2+1)>0,且
=24(k2+1)>0,且![]() ,
,![]() ,
,
设PQ的中点N(x0,y0),则![]() ,
, ,
,
∴N坐标为 ,
,![]() ,;
,;
因此直线ON的方程为![]() ,从而点M为
,从而点M为![]() ,又F1(﹣2,0),
,又F1(﹣2,0),
所以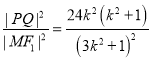 ,令u=3k2+1≥1,
,令u=3k2+1≥1,
则![]() ,
,
因此当u=4,即k=±1时h(u)最大值为3.
所以![]() 取得最大值
取得最大值![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.已知a2+c2=b2![]() ac.
ac.
(1)求cosB及tan2B的值;
(2)若b=3,A![]() ,求c的值.
,求c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆柱![]() 中,AB为圆
中,AB为圆![]() 的直径,
的直径,![]() 是
是![]() 的两个三等分点,EA,FC,GB都是圆柱
的两个三等分点,EA,FC,GB都是圆柱![]() 的母线.
的母线.
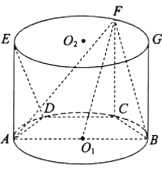
(1)求证:![]() 平面ADE;
平面ADE;
(2)设BC=1,已知直线AF与平面ACB所成的角为30°,求二面角A—FB—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们打印用的A4纸的长与宽的比约为![]() ,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为
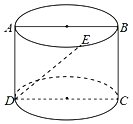
,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为![]() ,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.

其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图

以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() 在
在![]() 上存在两个极值点,求
上存在两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() ,
,![]() ,函数
,函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 线段的中点为
线段的中点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
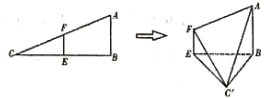
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com