
【题目】2019年春节前后,中国爆发新型冠状病毒(SARS-Cov-2)如图所示为1月24日至2月16日中国内地(除湖北以外的)感染新型冠状病毒新增人数的折线图,为了预测分析数据的变化规律,建立了![]() 与时间变量
与时间变量![]() 的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量
的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量![]() 的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:
的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:![]() ;根据2月4日至2月16日的数据(时间变量
;根据2月4日至2月16日的数据(时间变量![]() 的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:
的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:![]() .
.
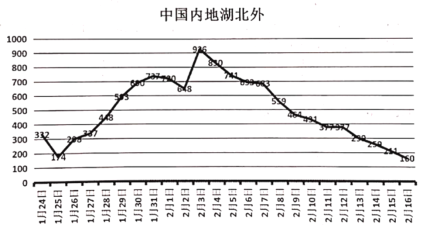
1月 24日 | 1月 25日 | 1月 26日 | 1月 27日 | 1月 28日 | 1月 29日 | 1月 30日 | 1月 31日 | 2月 1日 | 2月 2日 | 2月 3日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
332 | 174 | 298 | 337 | 448 | 593 | 690 | 737 | 720 | 648 | 926 |
2月 4日 | 2月 5日 | 2月 6日 | 2月 7日 | 2月 8日 | 2月 9日 | 2月 10日 | 2月 11日 | 2月 12日 | 2月 13日 | 2月 14日 | 2月 15日 | 2月 16日 |
12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
830 | 741 | 693 | 683 | 559 | 464 | 431 | 377 | 377 | 299 | 259 | 211 | 160 |
(1)求出两个回归直线方程;(计算结果取整数)
(2)中国政府为了人民的生命安全,听取专家意见,了解了病毒信息,并迅速做出一系列的隔离防护措施,但新冠状病毒在世界范围内爆发时,某些欧美国家采取放任的态度,不治疗、不隔离、不检测,甚至不公布,请你用以上数据说明采取一系列措施的必要性,不采取措施的后果.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: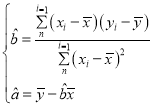 .
.
科目:高中数学 来源: 题型:
【题目】居民消费价格指数,简称CPI,是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.一般来说,CPI的高低直接影响着国家的宏观经济调控措施的出台与力度,下图是国家统计局发布的我国2009年至2018年这十年居民消费价格指数的折线图.
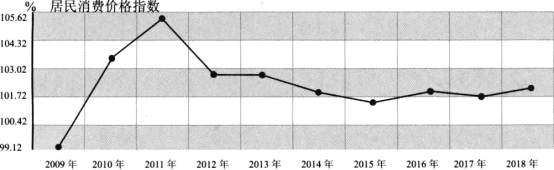
则下列对该折线图分析正确的是( )
A.这十年的居民消费价格指数的中位数为2013年的居民消费价格指数
B.这十年的居民消费价格指数的众数为2015年的居民消费价格指数
C.2009年~2012年这4年居民消费价格指数的方差小于2015年~2018年这4年居民消费价格指数的方差
D.2011年~2013年这3年居民消费价格指数的平均值大于2016年~2018年这3年居民消费价格指数的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .根据以上数据绘制
.根据以上数据绘制![]() 列联表,如下:
列联表,如下:
吸烟人数 | 非吸烟人数 | 总计 | |
重症人数 | 30 | 120 | 150 |
轻症人数 | 100 | 800 | 900 |
总计 | 130 | 920 | 1050 |
(1)根据列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症和吸烟有关?
的前提下认为新冠肺炎重症和吸烟有关?
(2)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.现有吸烟确诊患者20人,记这
万元.现有吸烟确诊患者20人,记这![]() 名患者的治疗费用总和为
名患者的治疗费用总和为![]() ,求
,求![]() .
.
附:
|
|
|
|
|
|
|
|
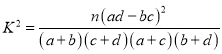
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公比大于0的等比数列{an}中,已知a3a5=a4,且a2,3a4,a3成等差数列.
(1)求{an}的通项公式;
(2)已知Sn=a1a2…an,试问当n为何值时,Sn取得最大值,并求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图一![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 在
在![]() 上,且
上,且![]() ,
,![]() 为
为![]() 中点,将
中点,将![]() 沿
沿![]() 折起,
折起,![]() 沿
沿![]() 折起,使得
折起,使得![]() ,
,![]() 重合于一点(如图二),设为
重合于一点(如图二),设为![]() .
.
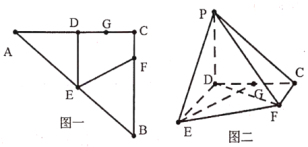
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知口袋里装有4个大小相同的小球,其中两个标有数字1,两个标有数字2.
(1)从口袋里任意取一球,求取到标有数字2的球的概率;
(2)第一次从口袋里任意取一球,放回口袋里后第二次再任意取一球,记第一次与第二次取到小球上的数字之和为![]() .当
.当![]() 为何值时,其发生的概率最大?说明理由.
为何值时,其发生的概率最大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了有效地加强高中生自主管理能力,推出了一系列措施,其中自习课时间的自主管理作为重点项目,学校有关处室制定了“高中生自习课时间自主管理方案”.现准备对该“方案”进行调查,并根据调查结果决定是否启用该“方案”,调查人员分别在各个年级随机抽取若干学生对该“方案”进行评分,并将评分分成![]() ,
,![]() ,
,![]() ,
,![]() 七组,绘制成如图所示的频率分布直方图.
七组,绘制成如图所示的频率分布直方图.
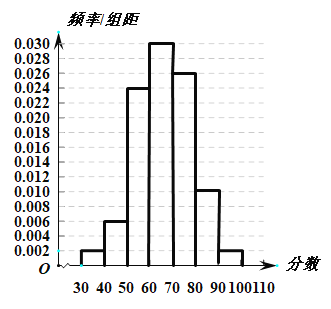
相关规则为①采用百分制评分,![]() 内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于
内认定为对该“方案”满意,不低于80分认定为对该“方案”非常满意,60分以下认定为对该“方案”不满意;②学生对“方案”的满意率不低于![]() 即可启用该“方案”;③用样本的频率代替概率.
即可启用该“方案”;③用样本的频率代替概率.
(1)从该校学生中随机抽取1人,求被抽取的这位同学非常满意该“方案”的概率,并根据频率分布直方图求学生对该“方案”评分的中位数.
(2)根据所学统计知识,判断该校是否启用该“方案”,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是直角梯形,AB=2CD=2PD=2,PC![]() ,且有PD⊥AD,AD⊥CD,AB∥CD.
,且有PD⊥AD,AD⊥CD,AB∥CD.

(1)证明:PD⊥平面ABCD;
(2)若四棱锥P﹣ABCD的体积为![]() ,求四棱锥P﹣ABCD的表面积.
,求四棱锥P﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 是等腰直角三角形.
是等腰直角三角形.
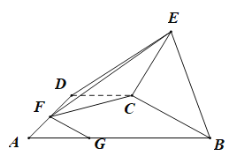
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(2)![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com