
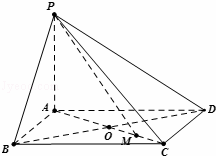
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
(I)求证:平面PBD⊥平面PAC;
(II)设AC与BD交于点O,M为OC中点,若二面角O﹣PM﹣D的正切值为![]() ,求a:b的值.
,求a:b的值.
考点:
平面与平面垂直的判定;与二面角有关的立体几何综合题.
专题:
综合题;空间向量及应用.
分析:
(I)根据线面垂直的判定,证明BD⊥平面PAC,利用面面垂直的判定,证明平面PBD⊥平面PAC.
(II)过O作OH⊥PM交PM于H,连HD,则∠OHD为A﹣PM﹣D的平面角,利用二面角O﹣PM﹣D的正切值为![]() ,即可求a:b的值.
,即可求a:b的值.
解答:
(I)证明:因为PA⊥平面ABCD,所以PA⊥BD
又ABCD为菱形,所以AC⊥BD,
因为PA∩AC=A,所以BD⊥平面PAC
因为BD⊂平面PBD,所以平面PBD⊥平面PAC.
(II)解:过O作OH⊥PM交PM于H,连HD

因为DO⊥平面PAC,由三垂线定理可得DH⊥PM,所以∠OHD为A﹣PM﹣D的平面角
又![]() ,且
,且![]()
从而
∴![]()
所以9a2=16b2,即![]() .
.
点评:
本题考查线面垂直、面面垂直的判定,考查面面角,解题的关键是掌握线面垂直、面面垂直的判定,作出面面角.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
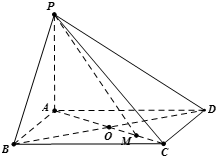 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.| 6 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市淮阴中学高三(下)期初数学试卷(解析版) 题型:解答题
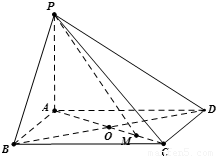 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.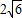 ,求a:b的值.
,求a:b的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年海南省琼海市嘉积中学高三(上)教学质量监测数学试卷(四)(理科)(解析版) 题型:解答题
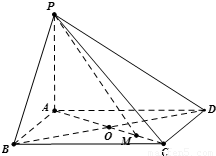 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.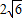 ,求a:b的值.
,求a:b的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市太湖二中高三(上)月考数学试卷(理科)(解析版) 题型:解答题
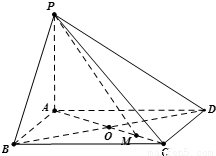 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b.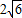 ,求a:b的值.
,求a:b的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com