
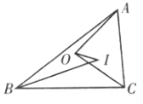
【题目】如图,已知![]() 分别是
分别是![]() 的外心、内心,
的外心、内心,![]() 与
与![]() 不重合,
不重合,![]() 在
在![]() 的内部或边上,且或者
的内部或边上,且或者![]() 在
在![]() 的内部或者
的内部或者![]() ,试求出使得等式
,试求出使得等式![]() 成立的一个充要条件(用关于
成立的一个充要条件(用关于![]() 的内角的条件表示)。
的内角的条件表示)。
【答案】见解析
【解析】
所求的充要条件是![]() 或
或![]()
充分性。
如图,若![]() ,则
,则![]() ,
,
![]()
![]() 。
。
从而,![]() 。
。
所以,![]() 四点共圆.
四点共圆.
故![]() .
.
于是,![]() .
.
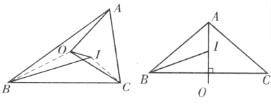
若![]() ,则
,则![]() 在
在![]() 的外部,如图,由题意知必有
的外部,如图,由题意知必有![]() 。由对称性可知
。由对称性可知![]() 三点共线,
三点共线,![]() ,且
,且![]() 在线段
在线段![]() 上.显然
上.显然
![]()
![]() .
.
故![]() .
.
必要性。
设![]() ,
,![]() 在
在![]() 的内部或边上。下面分两种情形讨论.
的内部或边上。下面分两种情形讨论.
1.若![]() ,则由对称性得
,则由对称性得![]() 三点共线,
三点共线,![]() 。因为
。因为![]() 在
在![]() 的内部或边上,所以,
的内部或边上,所以,![]() 必在线段
必在线段![]() 上(如图).
上(如图).
于是,![]() 。
。
代入![]() ,解得
,解得![]() .
.
2.若![]() 在
在![]() 的内部,则
的内部,则![]() 为锐角三角形.下证:必有
为锐角三角形.下证:必有![]() ,从而,
,从而,![]() 。为此分三种情形讨论.
。为此分三种情形讨论.
ⅰ.若![]() ,则
,则![]() ,这与
,这与![]() 为锐角三角形矛盾.
为锐角三角形矛盾.
ⅱ.若![]() ,则
,则![]() ,
,
![]() .
.
所以,![]() .
.
从而,![]() 在
在![]() 的外接圆的内部(如图),故
的外接圆的内部(如图),故![]() 。解得
。解得![]() ,这与
,这与![]() 矛盾.
矛盾.
ⅲ.若![]() ,类似ⅱ的推论过程得到
,类似ⅱ的推论过程得到![]() 矛盾.
矛盾.
故![]() ,
,![]() .
.
综上所述,![]() 的一个充要条件是
的一个充要条件是![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】现有形状、大小都相同的5张卡片,其中有2张卡片写着文字“中”,2张卡片写着文字“国”,1张卡片写着文字“梦”.若从中任意取出3张,则取出的3张卡片上的文字能组成“中国梦”的概率为____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了增强民众防控病毒的意识,举行了“预防新冠病毒知识竞赛”网上答题,随机抽取![]() 人,答题成绩统计如图所示.
人,答题成绩统计如图所示.
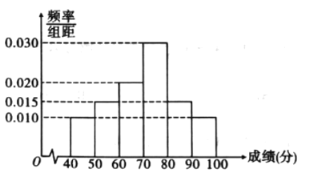
(1)由直方图可认为答题者的成绩![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() ,
,![]() 分别为答题者的平均成绩
分别为答题者的平均成绩![]() 和成绩的方差
和成绩的方差![]() ,那么这
,那么这![]() 名答题者成绩超过
名答题者成绩超过![]() 分的人数估计有多少人?(同一组中的数据用该组的区间中点值作代表)
分的人数估计有多少人?(同一组中的数据用该组的区间中点值作代表)
(2)如果成绩超过![]() 分的民众我们认为是“防御知识合格者”,用这
分的民众我们认为是“防御知识合格者”,用这![]() 名答题者的成绩来估计全市的民众,现从全市中随机抽取
名答题者的成绩来估计全市的民众,现从全市中随机抽取![]() 人,“防御知识合格者”的人数为
人,“防御知识合格者”的人数为![]() ,求
,求![]() .(精确到
.(精确到![]() )
)
附:①![]() ,
,![]() ;②
;②![]() ,则
,则![]() ,
,![]() ;③
;③![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为年龄层与热衷关心民生大事有关?
的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 12 | ||
中年 | 5 | ||
总计 | 30 |
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上台表演节目,则抽出的2人能胜任才艺表演的概率是多少?
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.己知
轴的非负半轴为极轴建立极坐标系.己知
点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为,
的参数方程为,![]() (
(![]() 为参数).曲线
为参数).曲线![]() 和曲线
和曲线![]() 相交于
相交于![]() 两点.
两点.
(1)求点![]() 的直角坐标;
的直角坐标;
(2)求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(3)求![]() 的面枳
的面枳![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某品牌饮料的某种食品添加剂是否超标,现对该品牌下的两种饮料一种是碳酸饮料![]() 含二氧化碳
含二氧化碳![]() ,另一种是果汁饮料
,另一种是果汁饮料![]() 不含二氧化碳
不含二氧化碳![]() 进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶
进行检测,现随机抽取了碳酸饮料、果汁饮料各10瓶![]() 均是
均是![]() 组成的一个样本,进行了检测,得到了如下茎叶图
组成的一个样本,进行了检测,得到了如下茎叶图![]() 根据国家食品安全规定当该种添加剂的指标大于
根据国家食品安全规定当该种添加剂的指标大于![]() 毫克
毫克![]() 为偏高,反之即为正常.
为偏高,反之即为正常.
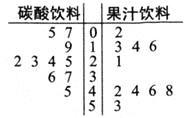
(1)依据上述样本数据,完成下列![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
的前提下认为食品添加剂是否偏高与是否含二氧化碳有关系?
正常 | 偏高 | 合计 | |
碳酸饮料 | |||
果汁饮料 | |||
合计 |
(2)现从食品添加剂偏高的样本中随机抽取2瓶饮料去做其它检测,求这两种饮料都被抽到的概率.
参考公式: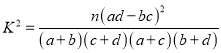 ,其中
,其中![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如下:
甲公司 | 乙公司 | |||||||||
职位 | A | B | C | D | 职位 | A | B | C | D | |
月薪/元 | 6000 | 7000 | 8000 | 9000 | 月薪/元 | 5000 | 7000 | 9000 | 11000 | |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | |
(1)根据以上信息,如果你是该求职者,你会选择哪一家公司?说明理由;
(2)某课外实习作业小组调查了1000名职场人士,就选择这两家公司的意愿做了统计,得到以下数据分布:
选择意愿 人员结构 | 40岁以上(含40岁)男性 | 40岁以上(含40岁)女性 | 40岁以下男性 | 40岁以下女性 |
选择甲公司 | 110 | 120 | 140 | 80 |
选择乙公司 | 150 | 90 | 200 | 110 |
若分析选择意愿与年龄这两个分类变量,计算得到的K2的观测值为k1=5.5513,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
附:![]()
| 0.050 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com