
【题目】如图,有三种类型的纸片(可翻转)。
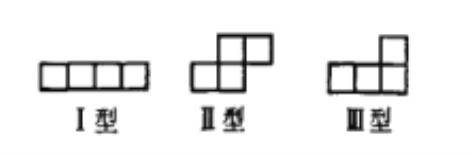
证明:(1)当![]() 时,
时,![]() 的纸板不能分割成若干个I型、II型的纸片;
的纸板不能分割成若干个I型、II型的纸片;
(2)当n为大于2的偶数时,![]() 的纸板可以分割成若干个II型、III型的纸片。
的纸板可以分割成若干个II型、III型的纸片。
【答案】(1)见解析;(2)见解析
【解析】
(1)用反证法证明.
假设![]() 纸板可以分割成u个I型、v个II型纸片.
纸板可以分割成u个I型、v个II型纸片.
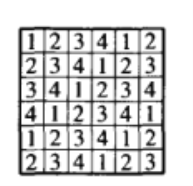
将![]() 纸板的各方格按图6方式从左上向右下标号.
纸板的各方格按图6方式从左上向右下标号.
接下来,将填有1、2、3、4的单元格依次记为![]() .则每个I型纸片包含
.则每个I型纸片包含![]() 各1个;每个II型纸片或包含
各1个;每个II型纸片或包含![]() 各1个,或包
各1个,或包![]() (或
(或![]() ,或
,或![]() ,或
,或![]() )各2个.
)各2个.
设上述II型纸片各有![]() 个.则所有纸片共包含
个.则所有纸片共包含
![]() 个,
个,![]() 个,
个,![]() 个,
个,![]() 个,其奇偶性相同.
个,其奇偶性相同.
但当![]() 时,
时,![]() 纸板上
纸板上![]() 各有
各有![]() 个,
个,![]() 有
有![]() 个,
个,![]() 有
有![]() 个,其奇偶性不同,矛盾.
个,其奇偶性不同,矛盾.
(2)用数学归纳法证明.
当![]() 时,如下图,命题成立.
时,如下图,命题成立.

假设可将n×n(n为大于2的偶数)纸板分割.则对(n+4)×(n+4)纸板,将其分成中心的n×n纸板及边上宽为2个方格的环.
如下图,可将环分割为若干个Ⅱ、Ⅲ型(以n=6为例,其余情况只需在各边增加若干个Ⅱ型纸片即可).中心的n×n纸板由归纳假设可以分割
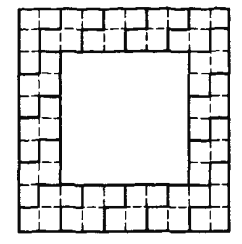
综上,命题成立.


科目:高中数学 来源: 题型:
【题目】在正方体的![]() 个顶点,
个顶点,![]() 个侧面(底面)的中心及体的中心共
个侧面(底面)的中心及体的中心共![]() 个点中,若由两两不同的且不共线的
个点中,若由两两不同的且不共线的![]() 个点构成的平面与由另外
个点构成的平面与由另外![]() 个不同点构成的直线垂直,则称这
个不同点构成的直线垂直,则称这![]() 个点为“正交
个点为“正交![]() 点组”,那么,由这
点组”,那么,由这![]() 个点形成的正交
个点形成的正交![]() 点组的总个数为( )
点组的总个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的命题是( )
A.已知随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]()
B.由独立性检验可知,有99%的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀
C.以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则c,k的值分别是
,则c,k的值分别是![]() 和0.3
和0.3
D.在回归分析模型中,残差平方和越大,说明模型的拟合效果越差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 是函数
是函数![]() 的导函数,则
的导函数,则![]() 的图象大致是( )
的图象大致是( )
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/8f50d3dfba9b485fac00e42a95909498.png] B. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/74ae44978a70424c961e850ed79072da.png]
C. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/2f113f7ec5294ba0bbd1f66b13f3e152.png] D. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/dbaa9025ccdb497380b769e5396c4c19.png]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2020年清明节前后3天每天下雨的概率为70%,通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率:用随机数![]() (
(![]() ,且
,且![]() )表示是否下雨:当
)表示是否下雨:当![]() 时表示该地区下雨,当
时表示该地区下雨,当![]() 时,表示该地区不下雨,从随机数表中随机取得20组数如下:
时,表示该地区不下雨,从随机数表中随机取得20组数如下:
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
(1)求出![]() 的值,并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率;
的值,并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率;
(2)从2011年开始到2019年该地区清明节当天降雨量(单位:![]() )如下表:(其中降雨量为0表示没有下雨).
)如下表:(其中降雨量为0表示没有下雨).
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明:从2011年开始至2020年, 该地区清明节有降雨的年份的降雨量![]() 与年份
与年份![]() 成线性回归,求回归直线
成线性回归,求回归直线![]() ,并计算如果该地区2020年(
,并计算如果该地区2020年(![]() )清明节有降雨的话,降雨量为多少?(精确到0.01)
)清明节有降雨的话,降雨量为多少?(精确到0.01)
参考公式: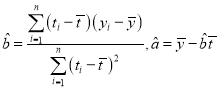 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD的一边CD内任取一点E,过E作对角线AC的平行线,交对角线BD于点G、交边AD于点H、交边BA的延长线于点F,联结BH交DF于点M.求证:
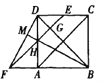
(1)C、G、M三点共线;
(2)C、E、M、F四点共圆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,
两点,![]() 是
是![]() 轴上的点,若
轴上的点,若![]() 是以
是以![]() 为斜边的等腰直角三角形, 求直线
为斜边的等腰直角三角形, 求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com