
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点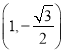 ,记椭圆
,记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,记
,记![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)椭圆![]() 的方程为
的方程为![]() (2)
(2)![]()
【解析】试题分析:
(1)由题意求得![]() ,
, ![]() ,
, ![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2)很明显直线的斜率存在,设出切线方程,联立直线与椭圆的方程,结合韦达定理得到关于实数![]() 的不等式组,结合不等式组的性质和题意讨论可得
的不等式组,结合不等式组的性质和题意讨论可得![]() .
.
试题解析:
(1)依题意, 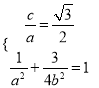 ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)依题意, ![]() ,
, ![]() ,直线
,直线![]() ,
,
设![]() ,则
,则![]() .
.
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得点
,得点![]() 的纵坐标为
的纵坐标为![]() ;
;
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得点
,得点![]() 的纵坐标为
的纵坐标为![]() ;
;
由题知,椭圆在点![]() 处切线斜率存在,可设切线方程为
处切线斜率存在,可设切线方程为![]() ,
,
由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
整理得: ![]() ,
,
将![]() ,
, ![]() 代入上式并整理得
代入上式并整理得![]() ,解得
,解得![]() ,
,
所以点![]() 处的切线方程为
处的切线方程为![]() .
.
令![]() 得,点
得,点![]() 的纵坐标为
的纵坐标为![]() ,
,
设![]() ,所以
,所以![]() ,
,
所以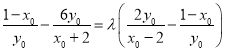 ,
,
所以 ,
,
将![]() 代入上式,
代入上式, ![]() ,因为
,因为![]() ,所以
,所以![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,DE⊥平面ABCD,AD∥BC,平面BCEF∩平面ADEF=EF,∠BAD=60°,AB=AD=2,DE=1. 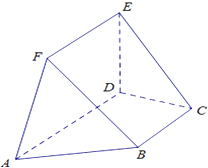
(1)求证:BC∥EF;
(2)求三棱锥B﹣ADE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在原点,离心率为 ![]() ,右焦点到直线x+y+
,右焦点到直线x+y+ ![]() =0的距离为2.
=0的距离为2.
(1)求椭圆E的方程;
(2)椭圆下顶点为A,直线y=kx+m(k≠0)与椭圆相交于不同的两点M、N,当|AM|=|AN|时,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,﹣4),且倾斜角为 ![]() ,圆C的极坐标方程为ρ=4cosθ.
,圆C的极坐标方程为ρ=4cosθ.
(1)求直线l的参数方程和圆C的直角坐标方程;
(2)若直线l和圆C相交于A、B两点,求|PA||PB|及弦长|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1.
,AB=2,PA=1. 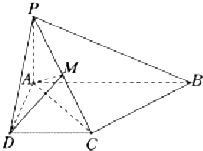
(1)求证:BC⊥平面PAC;
(2)若M是PC的中点,求二面角M﹣AD﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人6次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78 84
乙 78 82 88 82 95 90
(1)用茎叶图表示这两组数据,现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(2)若将频率视为概率,对运动员甲在今后三次测试成绩进行预测,记这三次成绩高于85分的次数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() 及方差
及方差![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,
(单位:元),继续购买该险种的投保人称为续保人,
续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 120 | 100 | 60 | 60 | 40 | 20 |
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的190%”.
求![]() 的估计值;
的估计值;
(III)求续保人本年度的平均保费估计值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com