Question

【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点．

（1）证明：BE∥平面ADP；
（2）求直线BE与平面PDB所成角的正弦值．

Answer 1

【答案】
（1）证明：如图，取PD中点M，连接EM，AM．

∵E，M分别为PC，PD的中点，∴EM∥DC，且EM= DC，

又由已知，可得EM∥AB，且EM=AB，

∴四边形ABEM为平行四边形，∴BE∥AM．

∵AM平面PAD，BE平面PAD，

∴BE∥平面ADP．

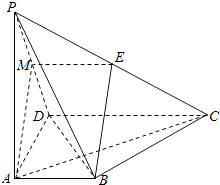
（2）解：连接BM，由（1）有CD⊥平面PAD，得CD⊥PD，

而EM∥CD，∴PD⊥EM．

又∵AD=AP，M为PD的中点，∴PD⊥AM，

∴PD⊥BE，∴PD⊥平面BEM，

∴平面BEM⊥平面PBD．

∴直线BE在平面PBD内的射影为直线BM，

∵BE⊥EM，∴∠EBM为锐角，

∴∠EBM为直线BE与平面PBD所成的角．

依题意，有PD=2 ，而M为PD中点，

∴AM= ，进而BE= ．

∴在直角三角形BEM中，sin∠EBM= = = ．

∴直线BE与平面PDB所成角的正弦值为 ．

【解析】（1）取PD中点M，连接EM，AM，推导出四边形ABEM为平行四边形，由此能证明BE∥平面ADP．（2）连接BM，推导出PD⊥EM，PD⊥AM，从而直线BE在平面PBD内的射影为直线BM，∠EBM为直线BE与平面PBD所成的角，由此能求出直线BE与平面PDB所成角的正弦值．