定义:设函数f(x)在(a,b)内可导,若f′(x)为(a,b)内的增函数,则称f(x)为(a,b)内的下凸函数.
(Ⅰ)已知f(x)=ex-ax3+x在(0,+∞)内为下凸函数,试求实数a的取值范围;
(Ⅱ)设f(x)为(a,b)内的下凸函数,求证:对于任意正数λ1,λ2,λ1+λ2=1,
不等式f(λ1x1+λ2x2)≤λ1f(x1)+λ2f(x2)对于任意的x1,x2∈(a,b)恒成立.
解:(I)f(x)=e
x-ax
3+x在(0,+∞)内为下凸函数等价于x∈(0,+∞)时,f′(x)=e
x-3ax
2+1为增函数;
所以x∈(0,+∞)时,[f′(x)]
′=e
x-6ax≥0恒成立,即
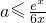
恒成立
设
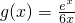
,
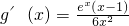
,
令g′(x)=0,得x=1,且当0<x<1时,g′(x)<0;当x>1时,g′(x)>0.
所以在x=1时,g(x)取得最小值为
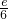
,所以

(II)证明:根据上凸函数的定义“f(x)是定义在闭区间[a,b]上的函数,若任意x,y∈[a,b]和任意λ∈(0,1),有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)成立”
取x=x
1,y=x
2,λ=λ
1,1-λ=1-λ
1=λ
2,而任意正数λ
1,λ
2,λ
1+λ
2=1,x
1、x
2∈(a,b)
得不等式f(λ
1x
1+λ
2x
2)≤λ
1f(x
1)+λ
2f(x
2)对于任意的x
1,x
2∈(a,b)恒成立.
分析:(I)函数f(x)在(0,+∞)内为下凸函数等价于x∈(0,+∞)时,f′(x)为增函数,则x∈(0,+∞)时,[f′(x)]
′≥0恒成立,将a分离出来,研究不等式另一侧的最小值即可求出a的范围.
(II)利用上凸函数的定义“f(x)是定义在闭区间[a,b]上的函数,若任意x,y∈[a,b]和任意λ∈(0,1),有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)成立”进行证明即可.
点评:本题主要考查了利用导数研究函数的单调性,以及利用上凸函数的定义证明不等式,属于难题.

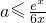 恒成立
恒成立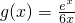 ,
,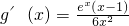 ,
,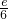 ,所以
,所以


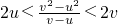 .
.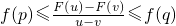 成立,则称F(x)是f(x)在区间I上的甲函数,f(x)是F(x)在区间I上的乙函数.
成立,则称F(x)是f(x)在区间I上的甲函数,f(x)是F(x)在区间I上的乙函数.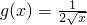 是
是 的乙函数.
的乙函数.