
����Ŀ�������ǵ������紫����Χ��㡢�����������������˶������й㷺�����Ӱ�죬���������������ϲ����
��1��Ϊ�����ѧ��ϲ�������Ƿ����Ա��йأ����ѡȡ50����ѧ�������ʾ����飬���ʾ����ֲ�����80������Ϊϲ���������ֵ���80������Ϊ��ϲ��������50����ѧ���ʾ����ֵĽ���þ�Ҷͼ��ʾ��ͼ��
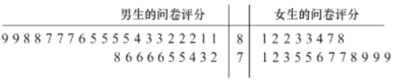
���������������������������
ϲ������ | ��ϲ������ | �ܼ� | |
�� |
|
|
|
���� |
|
|
|
�ܼ� |
|
|
|
�����Ƿ��� ![]() �İ�����Ϊϲ���������Ա��йأ�
�İ�����Ϊϲ���������Ա��йأ�
�ο���ʽ�����ݣ�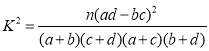 ��
��![]() ��
��
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
��2����֪ij�����ǹ���������ÿ��ƽ��������![]() ��ù��������ӹ���������ڹ����������������
��ù��������ӹ���������ڹ����������������![]() ������أ��������
������أ��������![]() ��
��![]() ��
��![]() ��
��![]()
������� | 9 |
| 6 |
| 3 |
ƽ�������� | 0.9 | 0.91 | 0.92 | 0.93 | 0.95 |
�����![]() ��
��![]() �����Իع鷽��
�����Իع鷽��![]() ����Ԥ������Ϊ1ʱ���������ʣ�
����Ԥ������Ϊ1ʱ���������ʣ�
�ο���ʽ�����ݣ�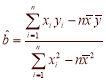 ��
��![]() ��
��![]() ��
��
���𰸡���1��û��![]() �İ�����Ϊϲ���������Ա��йأ���2��
�İ�����Ϊϲ���������Ա��йأ���2��![]() ��
��![]() ��
��
��������
��1��������ֱ����д�������ɣ����빫ʽ�����![]() �ɵý⣻
�ɵý⣻
��2��ת��������![]() ��
��![]() ���ټ����
���ټ����![]() ��
��![]() ��
��![]() ����빫ʽ���ɵ����Իع鷽�̣���
����빫ʽ���ɵ����Իع鷽�̣���![]() ��
��![]() ��ΪԤ��ֵ.
��ΪԤ��ֵ.
��1��������֪��![]() ��
��![]() ��
��![]() ��
��![]() ����д���������£�
����д���������£�
ϲ������ | ��ϲ������ | �ܼ� | |
�� | 8 | 12 | 20 |
���� | 20 | 10 | 30 |
�ܼ� | 28 | 22 | 100 |
����![]() ��
��
����û��![]() �İ�����Ϊϲ���������Ա��йأ�
�İ�����Ϊϲ���������Ա��йأ�
��2��������֪��![]() ��
��
��![]() ����
����![]() ��
��
���![]() ���������⣬��ȥ��
���������⣬��ȥ��
��![]() ����
����![]() ��
��
���![]() ��
��
���![]() ��
��![]() ��
��![]() ��
��
����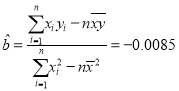 ��
��
![]()
����![]() ��
��![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() ��
��
����![]() ʱ��
ʱ��![]() ��
��
��Ԥ������Ϊ1ʱ����������Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ�мס��������豸����ͬһ�ֲ�Ʒ��Ϊ�˼�������豸�������������������������豸�����Ĵ�����Ʒ�и���ȡ��50����Ʒ��Ϊ���������һ������ָ��ֵ������������ָ��ֵ����![]() �ڣ���Ϊ�ϸ�Ʒ������Ϊ���ϸ�Ʒ. ��1�Ǽ����豸��������Ƶ���ֲ�����ͼ1�������豸��������Ƶ�ʷֲ�ֱ��ͼ.
�ڣ���Ϊ�ϸ�Ʒ������Ϊ���ϸ�Ʒ. ��1�Ǽ����豸��������Ƶ���ֲ�����ͼ1�������豸��������Ƶ�ʷֲ�ֱ��ͼ.
��1�������豸��������Ƶ���ֲ���
����ָ��ֵ | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
Ƶ�� | 1 | 4 | 19 | 20 | 5 | 1 |
ͼ1�������豸��������Ƶ�ʷֲ�ֱ��ͼ

��1����д�������������������������ж��Ƿ���90%�İ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ��ס��������豸��ѡ���йأ�
�����豸 | �����豸 | �ϼ� | |||||||||||||
�ϸ�Ʒ | |||||||||||||||
���ϸ�Ʒ | |||||||||||||||
�ϼ� | ���� |
P(K2��k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������
��������![]() ��
��![]() ��
��![]() ��
��![]() ����Բ��������ͬ�ĵ㣬FΪ���ҽ��㣬��
����Բ��������ͬ�ĵ㣬FΪ���ҽ��㣬��![]() ��
��![]() ��
��![]() �ɵȲ�����
�ɵȲ�����
��1������Բ�ķ��̣�
��2����![]() ��ֵ��
��ֵ��
��3�����߶�AC�Ĵ�ֱƽ������x�ύ��ΪD����ֱ��BD��б��k.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.���ȱ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ��
��![]() ��
��![]() Ҳ�ɵȱ�����.
Ҳ�ɵȱ�����.
B.��������![]() Ϊ
Ϊ![]() �ļ�ֵ�㣬��
�ļ�ֵ�㣬��![]() �����������������⣮
�����������������⣮
C.��![]() ������������
Ϊ������������![]() Ϊ���������ij�ֲ���Ҫ������
Ϊ���������ij�ֲ���Ҫ������
D.������![]() ��ʹ��
��ʹ��![]() ���ķ��ǣ���
���ķ��ǣ���![]() ��
��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Բ![]() ������
������![]() Ϊ���㣬
Ϊ���㣬![]() Ϊ����Բ�ģ��IJ�����������ı���
Ϊ����Բ�ģ��IJ�����������ı���![]() ����Բ
����Բ![]() ����������������������ҵ���Բ��Ҳ�������ϣ��������Ϊ�� ��
����������������������ҵ���Բ��Ҳ�������ϣ��������Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����
����![]() ���㣬
���㣬![]() Ϊ����ԭ��.
Ϊ����ԭ��.
��1������Բ![]() �ı����̣�
�ı����̣�
��2���趯ֱ��![]() ����Բ
����Բ![]() ���ҽ���һ�������㣬����Բ
���ҽ���һ�������㣬����Բ![]() �ཻ��
�ཻ��![]() ���㣬����ֱ��
���㣬����ֱ��![]() ��
��![]() ��б��֮��
��б��֮��![]() �Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ�˵������.
�Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϊ�˶�Ӧ���˿����仯����ɵ��Ͷ�����ȱ�����⣬�ⶨ��̨���ӳ�����������������Ϊ���˽����Ƕ����ӳ�����������������̬�ȣ�������粿���е��У����粿������������15��65����Ⱥ���������50�ˣ��������ݵ�Ƶ�ʷֲ�ֱ��ͼ��֧�����ӳ��������������������ͳ�ƽ�����£�
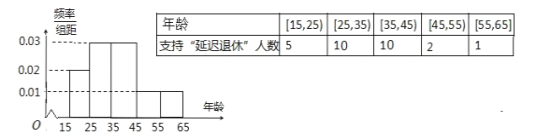
��1��������ͳ������������2��2�������������Ƿ���90%�İ�����Ϊ��45��Ϊ�ֽ������ӳ�����������������֧�ֶ��в��죺
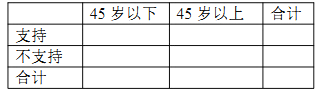
��2������������![]() �ı������������ѡȡ���˽��е��飬��ѡ�е�2����ǡ��1��֧�����ӳ��������ĸ���.
�ı������������ѡȡ���˽��е��飬��ѡ�е�2����ǡ��1��֧�����ӳ��������ĸ���.
�ο����ݣ�
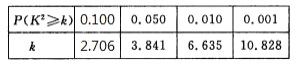
![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD��A1B1C1D1��,��BAD=��BCD=90��,��ADC=60����AD=CD,BB1��ƽ��ABCD,BB1=2AB=2.
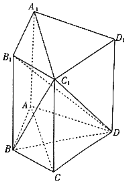
��1��֤��:AC��B1D.
��2����BC1��ƽ��B1C1D���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ���������У�����������У���ָ��ȫ�潨��С������������������ʺͳ��������̶Ƚϸߵij���.ȫ���������гƺ��Ƿ�ӳ�й���½������������ˮƽ����������ƺ�.Ϊ�ռ����֪ʶ������ȫ���������У�ij����֯����������֪ʶ�������������ȡ�˼ס���������λ��5��ְ���ijɼ�����λ���֣����±���

��1�������ϱ��е����ݣ��ֱ�����ס���������λ5��ְ���ijɼ���ƽ�����ͷ�����Ƚ��ĸ���λ��ְ������������֪ʶ���յø��ã�
��2���ü�������������ҵ�λ5��ְ���г�ȡ2�ˣ����ȡ��2��ְ���ijɼ���ľ���ֵ��С��4�ĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com