
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(1)求![]() 的顶点
的顶点![]() 的轨迹方程;
的轨迹方程;
(2)直线![]() 与顶点
与顶点![]() 的轨迹交于
的轨迹交于![]() 两点,当线段
两点,当线段![]() 的中点
的中点![]() 落在直线
落在直线![]() 上时,试问:线段
上时,试问:线段![]() 的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
的垂直平分线是否恒过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,P为
,P为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)设E为BC的中点,线段![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 平面
平面![]() ?若存在,求四棱锥
?若存在,求四棱锥![]() 的体积;若不存在,请说明理由.
的体积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在宽为![]() 的路边安装路灯,灯柱
的路边安装路灯,灯柱![]() 高为
高为![]() ,灯杆
,灯杆![]() 是半径为
是半径为![]() 的圆
的圆![]() 的一段劣弧.路灯采用锥形灯罩,灯罩顶
的一段劣弧.路灯采用锥形灯罩,灯罩顶![]() 到路面的距离为
到路面的距离为![]() ,到灯柱所在直线的距离为
,到灯柱所在直线的距离为![]() .设
.设![]() 为灯罩轴线与路面的交点,圆心
为灯罩轴线与路面的交点,圆心![]() 在线段
在线段![]() 上.
上.

(1)当![]() 为何值时,点
为何值时,点![]() 恰好在路面中线上?
恰好在路面中线上?
(2)记圆心![]() 在路面上的射影为
在路面上的射影为![]() ,且
,且![]() 在线段
在线段![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球比赛中,一队在本方罚球区内犯规,会被判罚点球,点球是进攻方非常有效的得分手段.研究机构对某位足球队员的1000次点球训练进行了统计分析,以帮助球员提高点球的命中率.如图,将球门框内的区域分成9个区域(区域代码为1—9,球门框外的区域记做区域0),统计球员射点球时射中10个区域次数和进球次数(即使射中球门框内,也可能被守门员扑出),得到如下的两个频率分布条形图:



(其中射中率![]() ,得分率
,得分率![]() )
)
(1)根据上述频率分布条形图,求射中球门框内时,各区域进球数的平均数(结果保留两位小数)和中位数;
(2)以该队员这1000次点球练习的进球频率作为他在比赛中射点球时进球的概率,设他在三次射点球时进球数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中, 平面
中, 平面![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在, 求
?若存在, 求![]() 的值;若不存在, 说明理由.
的值;若不存在, 说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年3月,国内新冠肺炎疫情得到有效控制,人们开始走出家门享受春光.某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
两个旅游团队计划游览该景点.若分别购票,则共需支付门票费1290元;若合并成个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为( )
A.20B.30C.35D.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.
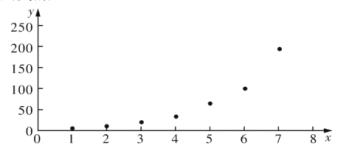
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次.
的回归方程,并预测活动推出第8天使用扫码支付的人次.
(3)推广期结束后,为更好的服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
人次 | 10 | 60 | 30 |
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调査结果发现:使用扫码支付的乘客中有5名乘客享受7折优惠,有10名乘客享受8折优惠,有15名乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: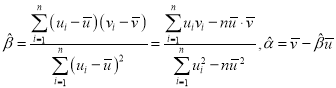 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁超市旗舰店在元旦当天推出一个购物满百元抽奖活动,凡是一次性购物满百元者可以从抽奖箱中一次性任意摸出2个小球(抽奖箱内共有5个小球,每个小球大小形状完全相同,这5个小球上分别标有1,2,3,4,5 这5个数字).
(1)列出摸出的2个小球的所有可能的结果.
(2)已知该超市活动规定:摸出的2个小球都是偶数为一等奖;摸出的2个小球都是奇数为二等奖.请分别求获得一等奖的概率与获得二等奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com