(1)证明不等式:

(2)已知函数

在

上单调递增,求实数

的取值范围。
(3)若关于x的不等式

在

上恒成立,求实数

的最大值。
(1)令
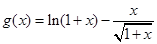
,
则
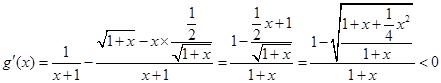
∴g(x)在

上单调递减,即g(x)<g(0),从而
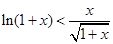
成立
(2)由
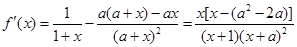
,当x=0或
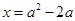
时,

,由已知得
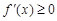
在

上恒成立,∴
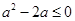
,又f(x)在

有意义,∴a≥0,综上:
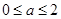
;
(3)由已知
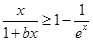
在

上恒成立,∵

,
当x>0时,易得
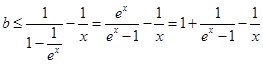
恒成立,
令
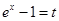
得
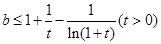
恒成立,由(2)知:令a=2得:
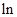
(1+x)>
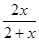
,
∴
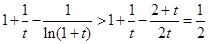
;
由(1)得:
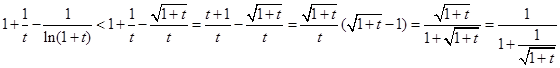
当
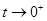
时,
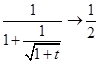
;∴当
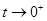
时,
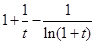
不大于
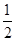
;∴
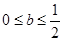
;
当x=0时,b∈R,综上:
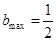
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
已知
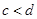
,
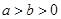
, 下列不等式中必然成立的一个是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知正数
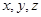
满足
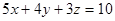
,
(1) 求证:
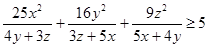
; (2) 求
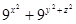
的最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在不等边△ABC中,
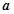
为最大边,如果
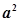
<
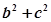
,则A的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知

,

,则下列有关

与

的大小关系表述正确的是______
①

; ②

; ③

(填正确的序号).
查看答案和解析>>


 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。 在
在 上恒成立,求实数
上恒成立,求实数 的最大值。
的最大值。