
����Ŀ�����о����� f �� x ��= ![]() ��
�� ![]() ������ʱ��ijͬѧ���������빫ʽ��������f��x������Ϊf��x��=
������ʱ��ijͬѧ���������빫ʽ��������f��x������Ϊf��x��= ![]() ��
�� ![]() �����������ں���f��x���������������
�����������ں���f��x���������������
�ٺ��� f��x����ͼ�������ĶԳ�ͼ�Σ�
�ں��� f��x����ͼ������Գ�ͼ�Σ�
�ۺ��� f��x����[0��6]������������
�ܺ��� f��x��û�����ֵҲû����Сֵ��
������mΪ��ʵ��������x�ķ��� f��x����m=0����ʵ������
����������ȷ���� ��
���𰸡��٢ۢ�
���������⣺���� f �� x ��= ![]() ��
�� ![]() =
= ![]() ��
�� ![]() ����ͼ��ʾ��P��x��0������A��0��2���ľ���|PA|�뵽��B��6��2���ľ���|PB|֮����ͼ�ο�֪����x=3����f��x��=0����6��PA��PB��6 �ຯ�� f��x����ͼ�������ĶԳ�ͼ�Σ��Գ�����Ϊ��3��0�����ʢ���ȷ���ڴ���
����ͼ��ʾ��P��x��0������A��0��2���ľ���|PA|�뵽��B��6��2���ľ���|PB|֮����ͼ�ο�֪����x=3����f��x��=0����6��PA��PB��6 �ຯ�� f��x����ͼ�������ĶԳ�ͼ�Σ��Գ�����Ϊ��3��0�����ʢ���ȷ���ڴ���
�ڣ����ޣ�+�ޣ�������ֵ��Ϊ����6��6��
�ʢۣ����� f��x����[0��6]��������������ȷ��
�ʢܺ��� f��x��û�����ֵҲû����Сֵ����ȷ��
�ʢ�����mΪ��ʵ��������x�ķ��� f��x����m=0������ʵ����������
���Դ��ǣ��٢ۢ�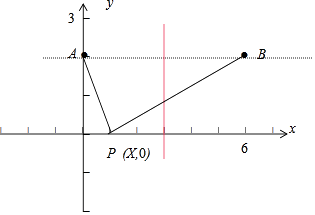
�����㾫����������Ҫ���������������ж���Ӧ�õ����֪ʶ�㣬��Ҫ�����������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɢ���������X�ķֲ���Ϊ
X | 1 | 2 | 3 |
P | P1 | P2 | P3 |
��EX=2�ij�Ҫ�����ǣ� ��
A.P1=P2
B.P2=P3
C.P1=P3
D.P1=P2=P3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����g��x��=a��x2�� ![]() ��x��e��eΪ��Ȼ�����ĵ�������h��x��=2lnx��ͼ���ϴ��ڹ���x��ԳƵĵ㣬��ʵ��a��ȡֵ��Χ�� ��
��x��e��eΪ��Ȼ�����ĵ�������h��x��=2lnx��ͼ���ϴ��ڹ���x��ԳƵĵ㣬��ʵ��a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������Լ����6�㵽��7��֮����ij�����棬��Լ�������絽Ӧ���Ұ�Сʱ�����һ����������ţ������絽����ȴ�����ס��������ܼ���ĸ��ʣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=a2lnx+ax��a��0����g��x��= ![]() 2tdt��F��x��=g��x����f��x����
2tdt��F��x��=g��x����f��x����
��1��������F��x���ĵ����ԣ�
��2����a��0ʱ����e2��F��x����1��e��x��[1��e]���������ʵ��a��ȡֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}�ǹ���Ϊ�����ĵȲ����У�a2�� a5�Ƿ���x2��12x+27=0 ����ʵ����������{bn}����3n��1bn=nan+1����n��1��an ��
������an��bn��
������TnΪ����{bn}��ǰn��ͣ���Tn �� ����Tn��7 ʱn�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ�����ë��ѡ�����У�ѡ��M��B1 �� B2 �� B3��λѡ�ֱַ����һ���Կ�������������α�����ͳ�ƣ�M��ʤ�ĸ��ʷֱ�Ϊ ![]() ���Ҹ�����������Ӱ�죮
���Ҹ�����������Ӱ�죮
��1����M���ٻ�ʤ�����ĸ��ʴ��� ![]() ����M��ѡ��һ�֣���������ѡ����M�Ƿ����ѡ��һ�֣�
����M��ѡ��һ�֣���������ѡ����M�Ƿ����ѡ��һ�֣�
��2����M��ʤ����X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OΪ����ԭ�㣬F��˫���� ![]() ���㣬A��B�ֱ�Ϊ�������Ҷ��㣬PΪ����һ�㣬��PF��x�ᣬ����A��ֱ��l���߶�PF���ڵ�M����y�ύ�ڵ�E��ֱ�� BM��y�ύ�ڵ�N����|OE|=2|ON|���� ����������Ϊ�� ��
���㣬A��B�ֱ�Ϊ�������Ҷ��㣬PΪ����һ�㣬��PF��x�ᣬ����A��ֱ��l���߶�PF���ڵ�M����y�ύ�ڵ�E��ֱ�� BM��y�ύ�ڵ�N����|OE|=2|ON|���� ����������Ϊ�� ��
A.3
B.2
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ρ�ABC����ȡһ��P�����P��A��B��C�ľ��붼���ڸ������α߳�һ��ĸ���Ϊ�� ��
A.1�� ![]()
B.1�� ![]()
C.1�� ![]()
D.1�� ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com