
(1)设不等式x2-2ax+a+2≤0的解集为M,如果M![]() [1,4],求实数a的取值范围?
[1,4],求实数a的取值范围?
(2)解关于x的不等式![]() >1(a≠1)。
>1(a≠1)。
(1)a的取值范围是(-1,![]() )(2)当a>1时解集为(-∞,
)(2)当a>1时解集为(-∞,![]() )∪(2,+∞);当0<a<1时,解集为(2,
)∪(2,+∞);当0<a<1时,解集为(2,![]() );当a=0时,解集为
);当a=0时,解集为![]() ;当a<0时,解集为(
;当a<0时,解集为(![]() ,2)。
,2)。
(1)M![]() [1,4]有两种情况:其一是M=
[1,4]有两种情况:其一是M=![]() ,此时Δ<0;其二是M≠
,此时Δ<0;其二是M≠![]() ,此时Δ=0或Δ>0,分三种情况计算a的取值范围
,此时Δ=0或Δ>0,分三种情况计算a的取值范围![]()
设f(x)=x2 -2ax+a+2,有Δ=(-2a)2-(4a+2)=4(a2-a-2)
当Δ<0时,-1<a<2,M=![]()
![]() [1,4];
[1,4];
当Δ=0时,a=-1或2;
当a=-1时M={-1}![]() [1,4];当a=2时,m={2}
[1,4];当a=2时,m={2}![]() [1,4]。
[1,4]。
当Δ>0时,a<-1或a>2。
设方程f(x)=0的两根x1,x2,且x1<x2,
那么M=[x1,x2],M![]() [1,4]
[1,4]![]() 1≤x1<x2≤4
1≤x1<x2≤4![]() ,
,
即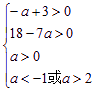 ,解得2<a<
,解得2<a<![]() ,
,
∴M![]() [1,4]时,a的取值范围是(-1,
[1,4]时,a的取值范围是(-1,![]() )。
)。
(2)原不等式可化为:![]() >0,
>0,
①当a>1时,原不等式与(x-![]() )(x-2)>0同解。
)(x-2)>0同解。
由于![]() ,
,
∴原不等式的解为(-∞,![]() )∪(2,+∞)。
)∪(2,+∞)。
②当a<1时,原不等式与(x-![]() )(x-2) <0同解。
)(x-2) <0同解。
由于![]() ,
,
若a<0,![]() ,解集为(
,解集为(![]() ,2);
,2);
若a=0时,![]() ,解集为
,解集为![]() ;
;
若0<a<1,![]() ,解集为(2,
,解集为(2,![]() )。
)。
综上所述:当a>1时解集为(-∞,![]() )∪(2,+∞);当0<a<1时,解集为(2,
)∪(2,+∞);当0<a<1时,解集为(2,![]() );当a=0时,解集为
);当a=0时,解集为![]() ;当a<0时,解集为(
;当a<0时,解集为(![]() ,2)。
,2)。


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| x |
| 8 |
| a+b |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011年高三数学一轮精品复习学案:6.3 单元总结与测试(解析版) 题型:解答题
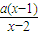 >1(a≠1).
>1(a≠1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com