
数列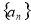 满足:
满足: ,
,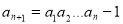 (
(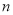 ≥3),记
≥3),记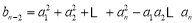
(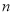 ≥3).
≥3).
(1)求证数列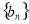 为等差数列,并求通项公式;
为等差数列,并求通项公式;
(2)设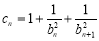 ,数列{
,数列{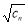 }的前n项和为
}的前n项和为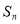 ,求证:
,求证: <
<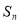 <
<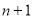 .
.
(1)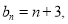 (2)详见解析.
(2)详见解析.
【解析】
试题分析:(1)本题实质由和项求通项:
当n≥3时,因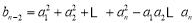 ①, 故
①, 故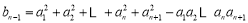 ②,
②,
②-①,得 bn-1-bn-2=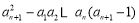 =
=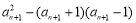 =1,为常数,所以,数列{bn}为等差数列因 b1=
=1,为常数,所以,数列{bn}为等差数列因 b1=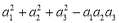 =4,故
=4,故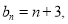 (2)本题证明实质是求和,而求和关键在于对
(2)本题证明实质是求和,而求和关键在于对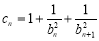 开方:因
开方:因 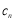
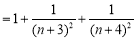
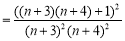 ,
,
故 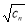
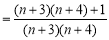

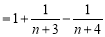 .
.
所以 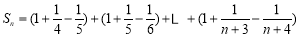
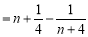 ,即 n<Sn
,即 n<Sn
又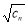 <
<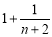 ,于是
,于是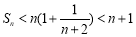 . 于是
. 于是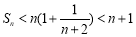
解 (1)方法一 当n≥3时,因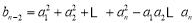 ①,
①,
故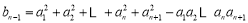 ② 2分
② 2分
②-①,得 bn-1-bn-2=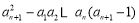 =
=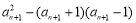 =1,为常数,所以,数列{bn}为等差数列 5分
=1,为常数,所以,数列{bn}为等差数列 5分
因 b1=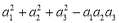 =4,故
=4,故 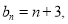 8分
8分
方法二 当n≥3时,a1a2an=1+an+1, a1a2anan+1=1+an+2, 将上两式相除并变形,得 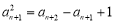 ------2分 于是,当n∈N*时,
------2分 于是,当n∈N*时, 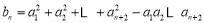

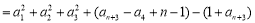
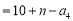 . 5分
. 5分
又a4=a1a2a3-1=7,故bn=n+3(n∈N*).
所以数列{bn}为等差数列,且bn=n+3 8分
(2) 因 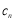
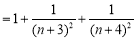
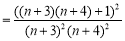 , 10分
, 10分
故 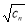
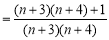

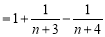 . 12分
. 12分
所以 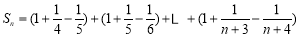
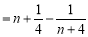 ,
,
即 n<Sn 。 14分
又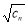 <
<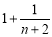 ,于是
,于是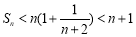 . 于是
. 于是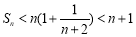 .---16分
.---16分
考点:等差数列定义,裂项求和


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测文科数学试卷(解析版) 题型:填空题
已知圆柱的底面半径为1,母线长与底面的直径相等,则该圆柱的表面积为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试理科数学试卷(解析版) 题型:填空题
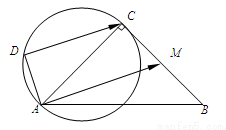
如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则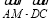 的最大值是 .
的最大值是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试理科数学试卷(解析版) 题型:填空题
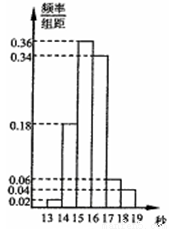
某学校为了解该校600名男生的百米成绩(单位:s),随机选择了50名学生进行调查,
下图是这50名学生百米成绩的频率分布直方图。根据样本的频率分布,估计这600名学生中成绩在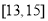 (单位:s)内的人数大约是 .
(单位:s)内的人数大约是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:解答题
在四棱锥P-ABCD中,AB∥DC,AB⊥平面PAD, PD=AD,AB=2DC,E是PB的中点.

求证:(1)CE∥平面PAD;
(2)平面PBC⊥平面PAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com