
【题目】已知函数![]() .
.
(1)讨论![]() 的单调区间;
的单调区间;
(2)当![]() 且
且![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析(2)证明见解析
【解析】
(1)函数![]() 定义域为
定义域为![]() ,求出导函数,通过
,求出导函数,通过![]() ,
,![]() ,
,![]() 判断导函数符号,求解函数的单调区间;(2)运用分析法转化证明,要证,只需证,法一中要证
判断导函数符号,求解函数的单调区间;(2)运用分析法转化证明,要证,只需证,法一中要证![]() ,只需证:
,只需证:![]() ,令
,令![]() ,求导判断导数值符号即可;法二中只需证
,求导判断导数值符号即可;法二中只需证![]() ,设
,设![]() ,
,![]() ,
,![]() 在
在![]() 上恒成立,求出
上恒成立,求出![]() ,
,![]() 的最值进行比较即可;法三中只需证:
的最值进行比较即可;法三中只需证:![]() .设
.设![]() ,判断
,判断![]() ,函数
,函数![]() 单调递增,
单调递增,![]() ,证明即可.
,证明即可.
(1)函数![]() 定义域为
定义域为![]() ,
,
![]()
![]() .
.
①若![]() 时,则
时,则![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
②若![]() 时,
时,![]() ,令
,令![]() 或
或![]() .
.
又![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
③若![]() 时,
时,![]() ,
,
令![]() 或
或![]() .
.
又![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(2)法一:![]() ,
,![]() ,
,
要证![]() ,只需证
,只需证![]() ,
,
只需证:![]() ,
,
只需证:![]() ,设
,设![]() ,
,
即![]() ,
,
![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即原不等式成立.
,即原不等式成立.
法二:要证![]() ,只需证
,只需证![]() ,
,
![]() ,只需证
,只需证![]() ,
,
设![]() ,
,![]() ,
,
![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以当![]() 时,
时,![]() ,
,
即原不等式成立.
法三:![]() ,
,![]() .
.
要证:![]() 成立,
成立,
只需证:![]() .
.
设![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() .
.
即原不等式成立.


科目:高中数学 来源: 题型:
【题目】随着国内电商的不断发展,快递业也进入了高速发展时期,按照国务院的发展战略布局,以及国家邮政管理总局对快递业的宏观调控,SF快递收取快递费的标准是:重量不超过1kg的包裹收费10元;重量超过1kg的包裹,在收费10元的基础上,每超过1kg(不足1kg,按1kg计算)需再收5元.某县SF分代办点将最近承揽的100件包裹的重量统计如下:
重量(单位:kg) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
件数 | 43 | 30 | 15 | 8 | 4 |
对近60天,每天揽件数量统计如下表:
件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
件数 | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 1 | 6 |
以上数据已做近似处理,将频率视为概率.
(1)计算该代办未来5天内不少于2天揽件数在101~300之间的概率;
(2)①估计该代办点对每件包裹收取的快递费的平均值;
②根据以往的经验,该代办点将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前该代办点前台有工作人员3人,每人每天揽件不超过150件,日工资110元.代办点正在考虑是否将前台工作人员裁减1人,试计算裁员前后代办点每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场营销人员对某商品![]() 进行市场营销调查,发现每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到下表:
进行市场营销调查,发现每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到下表:
回馈点数 | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析发现,可用线性回归模型拟合该商品每天的销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若回馈6个点时该商品每天销量;
,并预测若回馈6个点时该商品每天销量;
(2)已知节日期间某地拟购买该商品的消费群体十分庞大,营销调研机构对其中的200名消费者的返点数额的心理预期值进行了抽样调查,得到如下频数表:
返还点数预期值区间 |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位拟购买该商品的消费者对返点点数的心理预期值的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0.1);
(ii)将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望紧缩型”消费者的人数为随机变量
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望紧缩型”消费者的人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式及数据:①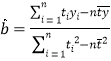 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() 倍(纵坐标不变)得到函数
倍(纵坐标不变)得到函数![]() 的图像,则下列说法正确的是( )
的图像,则下列说法正确的是( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
D. ![]() 是函数
是函数![]() 的一条对称轴
的一条对称轴
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 前n项和为
前n项和为![]() ,且
,且![]() 其中m为实常数,
其中m为实常数,![]() 且
且![]() .
.
(1)求证:![]() 是等比数列;
是等比数列;
(2)若数列![]() 的公比满足
的公比满足![]() 且
且![]() ,
,![]() ,求证:数列
,求证:数列![]() 是等差数列,并求
是等差数列,并求![]() 的通项公式;
的通项公式;
(3)若![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n和
的前n和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长![]() (单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
(单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.

(1)求图中![]() 的值;
的值;
(2)估计该校担任班主任的教师月平均通话时长的中位数;
(3)在![]() ,
,![]() 这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com