
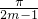
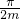
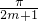
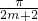
 .由点P是双曲线x2-y2=a2上的点,得n2=m2-a2,整理得KPA•KPB=1.由斜率与倾斜角的关系,得tanα•tanβ=1,结合三角函数诱导公式,得α+β=
.由点P是双曲线x2-y2=a2上的点,得n2=m2-a2,整理得KPA•KPB=1.由斜率与倾斜角的关系,得tanα•tanβ=1,结合三角函数诱导公式,得α+β= ,最后根据β=mα化简整理,即可得到本题的答案.
,最后根据β=mα化简整理,即可得到本题的答案. 解:∵双曲线方程为x2-y2=a2,即
解:∵双曲线方程为x2-y2=a2,即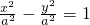 (a>0)
(a>0)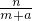 ;直线PB的斜率为KPB=
;直线PB的斜率为KPB=
 …(1)
…(1) ,解之得α=
,解之得α=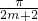


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com