
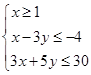
 =-
=- .
.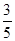 .
. ,34]
,34]
 ,得A(1,
,得A(1, ).
).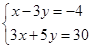 ,得B(5,3).
,得B(5,3). ,得C(1,
,得C(1, ).
). =-
=- .
.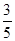 ,∴-a=-
,∴-a=-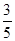 ,∴a=
,∴a=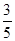 .
. 为(x,y)与原点(0,0)的距离,结合不等式的区域,易知A点到原点距离最小为
为(x,y)与原点(0,0)的距离,结合不等式的区域,易知A点到原点距离最小为 ,最大值为|OB|、|OC|、原点O到直线3x+5y=30距离三者之一,计算得,最大值为|OB|=
,最大值为|OB|、|OC|、原点O到直线3x+5y=30距离三者之一,计算得,最大值为|OB|= .故z=x2+y2的取值范围是[
.故z=x2+y2的取值范围是[ ,34].
,34].

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com