
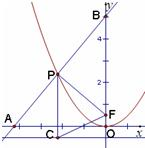
 已知椭圆4x2+3y2=3,抛物线的开口向上,且其顶点在椭圆C的中心,焦点为椭圆的一个焦点F.点P为抛物线上的一点,PC垂直于直线y=-
已知椭圆4x2+3y2=3,抛物线的开口向上,且其顶点在椭圆C的中心,焦点为椭圆的一个焦点F.点P为抛物线上的一点,PC垂直于直线y=-| 1 | 2 |
| x2 | ||||
(
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 6 |
| 3 |
| 3 |
| 2 |
| ||||
| x0 |
| x02-1 |
| 2x0 |
| 2x0 |
| x02-1 |
| 2x0 |
| x02-1 |
| 1 |
| 2 |
| x2 | ||||
(
|
12-(
|
| 1 |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 1 |
| 6 |
| 3 |
| 3 |
| 2 |
| ||||
| x0 |
| x02-1 |
| 2x0 |
| 2x0 |
| x02-1 |
| 2x0 |
| x02-1 |
| 1 |
| 2 |
| 2x0 |
| x02-1 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2x0 |
| x02-1 |
| 1 |
| 2 |
| x02(x02+3) |
| 2(x02-1) |
| x02(x02+3) |
| 2(x02-1) |
| 1 |
| 4 |
| x02(x02+3) |
| 2(x02-1) |
| 5 |
| 5 |
| 5 |
| 2 |


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
4
| ||
| 5 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:江西省白鹭洲中学2010-2011学年高二下学期第三次月考数学理科试题 题型:044
已知椭圆4x2+3y2=3,抛物线的开口向上,且其顶点在椭圆C的中心,焦点为椭圆的一个焦点F.点P为抛物线上的一点,PC垂直于直线l:![]() ,垂足为C,已知直线AB垂直PF分别交x、y轴于A、B.
,垂足为C,已知直线AB垂直PF分别交x、y轴于A、B.

(1)是否存在点P,使△PCF为等腰直角三角形,若存在求出点P,若不存在说明理由;
(2)是否存在点P,使P平分线段AB,若存在求出点P,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考数学冲刺预测试卷01(理科)(解析版) 题型:解答题
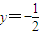 ,垂足为C,已知直线AB垂直PF分别交x、y轴于A、B.
,垂足为C,已知直线AB垂直PF分别交x、y轴于A、B.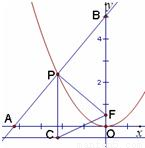
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com