
设不等式 的解集为
的解集为 ,
, .
.
(Ⅰ)证明: ;
;
(Ⅱ)比较 与
与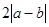 的大小,并说明理由.
的大小,并说明理由.
(Ⅰ)见解析(Ⅱ)|1-4ab|>2|a-b|
解析试题分析:(Ⅰ)利用零点分析法将f(x)=|x-1|-|x+2|化为分段函数,根据分段函数的值域,将不等式 化为不等式-2<-2x-1<0,解得集合M,由
化为不等式-2<-2x-1<0,解得集合M,由 从而得出
从而得出 的取值范围,利用含绝对值不等式性质及
的取值范围,利用含绝对值不等式性质及 的取值范围,利用放缩法,即可推出所证不等式
的取值范围,利用放缩法,即可推出所证不等式 ;(Ⅱ)先用作出比较法比较|1-4ab|2与4|a-b|2的大小,再利用不等式的开方性质,即可比较出
;(Ⅱ)先用作出比较法比较|1-4ab|2与4|a-b|2的大小,再利用不等式的开方性质,即可比较出 与
与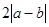 的大小.
的大小.
试题解析:(Ⅰ)记f(x)=|x-1|-|x+2|=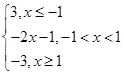
由-2<-2x-1<0解得- <x<
<x< ,则M=(-
,则M=(- ,
, ). 3分
). 3分
所以| a+
a+ b|≤
b|≤ |a|+
|a|+ |b|<
|b|< ×
× +
+ ×
× =
= . 6分
. 6分
(Ⅱ)由(Ⅰ)得a2< ,b2<
,b2< .
.
因为|1-4ab|2-4|a-b|2=(1-8ab+16a2b2)-4(a2-2ab+b2)
=(4a2-1)(4b2-1)>0, 9分
所以|1-4ab|2>4|a-b|2,故|1-4ab|>2|a-b|. 10分
考点:含绝对值不等式解法,含绝对值不等式性质,放缩法,比较法,不等式性质,运算求解能力,转化与化归思想,分类整合思想


科目:高中数学 来源: 题型:填空题
下面四个命题:①若a>b,c>1,则algc>blgc;
②若a>b,c>0,则algc>blgc;
③若a>b,则a·2c>b·2c;
④若a<b<0,c>0,则 >
> .
.
其中正确命题有 .(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com