
【题目】在四棱锥S-ABCD中,底面ABCD是边长为1的正方形,SD![]() 底面ABCD,SD=2,其中
底面ABCD,SD=2,其中![]() 分别是
分别是![]() 的中点,
的中点,![]() 是
是![]() 上的一个动点.
上的一个动点.
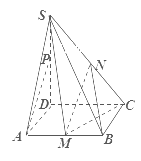
(1)当点![]() 落在什么位置时,
落在什么位置时,![]() ∥平面
∥平面![]() ,证明你的结论;
,证明你的结论;
(2)求三棱锥![]() 的体积.
的体积.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者.(13分)
(1)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;
(2)从图中A,B,C,D四人中随机选出两人,记ξ为选出的两人中指标x的值大于1.7的人数,求ξ的分布列和数学期望E(ξ);
(3)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°. (Ⅰ)证明:直线BC∥平面PAD;
AD,∠BAD=∠ABC=90°. (Ⅰ)证明:直线BC∥平面PAD;
(Ⅱ)若△PAD面积为2 ![]() ,求四棱锥P﹣ABCD的体积.
,求四棱锥P﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有下面四个命题
p1:若复数z满足 ![]() ∈R,则z∈R;
∈R,则z∈R;
p2:若复数z满足z2∈R,则z∈R;
p3:若复数z1 , z2满足z1z2∈R,则z1= ![]() ;
;
p4:若复数z∈R,则 ![]() ∈R.
∈R.
其中的真命题为( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其
范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.
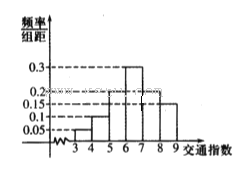
(1)请补全直方图,并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个?
(2)用分层抽样的方法从交通指数在[4,6),[6,8),[8,l0]的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽出的6个路段中任取2个,求至少一个路段为轻度拥堵的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1,
=1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.(12分)
)中恰有三点在椭圆C上.(12分)
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为﹣1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知sinB+sinA(sinC﹣cosC)=0,a=2,c= ![]() ,则C=( )
,则C=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com