
定义在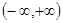 上的偶函数
上的偶函数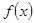 满足
满足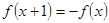 ,且在
,且在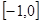 上是增函数,下面关于
上是增函数,下面关于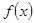 的判断:
的判断:
①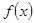 关于点P(
关于点P(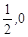 )对称
②
)对称
②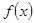 的图像关于直线
的图像关于直线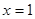 对称;
对称;
③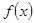 在[0,1]上是增函数;
④
在[0,1]上是增函数;
④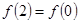 .
.
其中正确的判断是_________(把你认为正确的序号都填上)
①、②、④
【解析】
试题分析:由f(x)为偶函数可得f(-x)=f(x),由f(x+1)=-f(x)可得f(1+x)=-f(-x),则f(x)图象关于点P(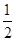 ,0)对称,即①正确;
,0)对称,即①正确;
f(x)图象关于y轴(x=0)对称,故x=1也是图象的一条对称轴,故②正确;
由f(x)为偶函数且在[-1,0]上单增可得f(x)在[0,1]上是减函数,即③错;
由f(x+1)=-f(x)可得f(2+x)=-f(x+1)=f(x),∴f(2)=f(0),即④正确。故答案为:①②④
考点:函数的对称性,函数的单调性,函数奇偶性的应用。
点评:中档题,本题具有一定综合性,要求对函数的对称性、单调性、奇偶性熟练掌握并灵活运用,对考查学生的数形结合思想很有帮助。


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源:2012届浙江省杭州学军中学高三第一次月考理科数学 题型:填空题
定义在 上的偶函数
上的偶函数 满足
满足 ,且在
,且在 上是增函数,下面是关于f(x)的判断
上是增函数,下面是关于f(x)的判断 :
:
① 关于点P(
关于点P( )对称 ②
)对称 ② 的图像关于直线
的图像关于直线 对称;
对称;
③ 在[0,1]上是增函数; ④
在[0,1]上是增函数; ④ .
.
其中正确的判断是_____________________(把你认为正确的判断都填上)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建莆田一中高三上学期第一学段考试文科数学试卷(解析版) 题型:填空题
已知定义在 上的偶函数满足:
上的偶函数满足: ,且当
,且当 时,
时, 单调递减,给出以下四个命题:①
单调递减,给出以下四个命题:① ;②
;② 是函数
是函数 图像的一条对称轴;③函数
图像的一条对称轴;③函数 在区间
在区间 上单调递增;④若方程
上单调递增;④若方程 .在区间
.在区间 上有两根为
上有两根为 ,则
,则 。以上命题正确的是 。(填序号)
。以上命题正确的是 。(填序号)
查看答案和解析>>
科目:高中数学 来源:2015届山西省高一下学期期中考试数学试卷(解析版) 题型:选择题
定义在 上的偶函数
上的偶函数 满足
满足 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则
是钝角三角形的两个锐角,则 与
与 的大小关系是
的大小关系是
A. B.
B.
C. D.
D.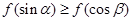
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省高三九月诊断考试理科数学 题型:填空题
已知定义在 上的偶函数
上的偶函数 满足:
满足: 且在区间
且在区间 上
上
单调递增,那么,下列关于此函数 性质的表述:
性质的表述:
①函数 的图象关于直线
的图象关于直线 对称; ②函数
对称; ②函数 是周期函数;
是周期函数;
③当 时,
时, ; ④函数
; ④函数 的图象上横坐标为偶数的点都是函数的极小值点。 其中正确表述的番号是
.
的图象上横坐标为偶数的点都是函数的极小值点。 其中正确表述的番号是
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com