
【题目】公元2020年春,我国湖北武汉出现了新型冠状病毒,人感染后会出现发热、咳嗽、气促和呼吸困难等,严重的可导致肺炎甚至危及生命.为了尽快遏制住病毒的传播,我国科研人员,在研究新型冠状病毒某种疫苗的过程中,利用小白鼠进行科学试验.为了研究小白鼠连续接种疫苗后出现![]() 症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为
症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为![]() ,假设每次接种后当天是否出现
,假设每次接种后当天是否出现![]() 症状与上次接种无关.
症状与上次接种无关.
(1)若某只小白鼠出现![]() 症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
(2)若某只小白鼠在一个接种周期内出现2次或3次![]() 症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为
症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
(1)利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出实验至多持续一个接种周期的概率;
(2)设事件![]() 为“在一个接种周期内出现2次或3次
为“在一个接种周期内出现2次或3次![]() 症状”,分别求出
症状”,分别求出![]() ,
,![]() ,
,![]() ,由此能求出
,由此能求出![]() 的分布列和数学期望.
的分布列和数学期望.
(1)已知每只小白鼠接种后当天出现![]() 症状的概率均为
症状的概率均为![]() ,且每次试验间相互独立,所以,一只小白鼠第一天接种后当天出现
,且每次试验间相互独立,所以,一只小白鼠第一天接种后当天出现![]() 症状的概率为
症状的概率为![]()
在第二天接种后当天出现![]() 症状的概率为:
症状的概率为:![]()
能参加第三天试验但不能参加下一个接种同期的概率为:![]() ,
,
∴一只小白鼠至多参加一个接种周期试验的概率为:
![]() ;
;
(2)设事件![]() 为“在一个接种周期内出现2次或3次
为“在一个接种周期内出现2次或3次![]() 症状”,则
症状”,则
![]() ;
;
随机变量![]() 可能的取值为1,2,3,则
可能的取值为1,2,3,则
![]()
![]()
![]() ;
;
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
随机变量![]() 的数学期望为:
的数学期望为:
![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知王明比较喜爱打篮球,近来,他为了提高自己的投篮水平,制定了一个夏季训练计划.班主任为了了解其训练效果,开始训练前,统计了王明![]() 场比赛的得分,计算出得分数据的中位数为
场比赛的得分,计算出得分数据的中位数为![]() 分,平均得分为
分,平均得分为![]() 分,得分数据的方差为
分,得分数据的方差为![]() ,训练结束后统计了
,训练结束后统计了![]() 场比赛得分成绩茎叶图如下图:
场比赛得分成绩茎叶图如下图:
![]()
(1)求王明训练结束后统计的![]() 场比赛得分的中位数,平均得分以及方差;
场比赛得分的中位数,平均得分以及方差;
(2)若只从训练前后统计的各![]() 场比赛得分数据分析,训练计划对王明投篮水平的提高是否有帮助?
场比赛得分数据分析,训练计划对王明投篮水平的提高是否有帮助?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是一块平行四边形园地![]() ,经测量,
,经测量,![]()
![]() .拟过线段
.拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计直路的宽度),将该园地分为面积之比为
的边上,不计直路的宽度),将该园地分为面积之比为![]() 的左,右两部分分别种植不同花卉.设
的左,右两部分分别种植不同花卉.设![]() (单位:m).
(单位:m).

(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)试确定点![]() 的位置,使直路
的位置,使直路![]() 的长度最短.
的长度最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构为了了解某产品年产量x(吨)对价格y(千克/吨)和利润z的影响,对近五年该产品的年产量和价格统计如下表:
x | 1 | 2 | 3 | 4 | 5 |
y | 17.0 | 16.5 | 15.5 | 13.8 | 12.2 |
(1)求y关于x的线性回归方程![]() ;
;
(2)若每吨该产品的成本为12千元,假设该产品可全部卖出,预测当年产量为多少时,年利润w取到最大值?
参考公式: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取了100名高中生,根据问卷调查,得到以下数据:
作文成绩优秀 | 作文成绩一般 | 总计 | |
课外阅读量较大 | 35 | 20 | 55 |
课外阅读量一般 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
(1)根据列联表,能否有99.5%的把握认为课外阅读量的大小与作文成绩优秀有关;
(2)若用分层抽样的方式从课外阅读量一般的高中生中选取了6名高中生,再从这6名高中生中随机选取2名进行面谈,求面谈的高中生中至少有1名作文成绩优秀的概率.
附: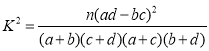 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.


(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com