
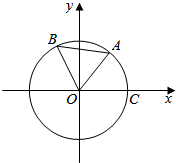
 如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,角∠AOB=$\frac{π}{4}$,若点A的坐标为($\frac{\sqrt{2}}{10}$,$\frac{7\sqrt{2}}{10}$),记∠COA=α.
如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,角∠AOB=$\frac{π}{4}$,若点A的坐标为($\frac{\sqrt{2}}{10}$,$\frac{7\sqrt{2}}{10}$),记∠COA=α.分析 (Ⅰ)由已知,根据三角函数的定义可求sinα,cosα的值,利用二倍角公式即可计算得解.
(Ⅱ)利用特殊角的三角函数值,两角和的正弦函数余弦函数公式分别求出cos∠COB,sin∠COB的值即可得解.
解答 (本题满分为12分)
解:(Ⅰ)∵A的坐标为($\frac{\sqrt{2}}{10}$,$\frac{7\sqrt{2}}{10}$),根据三角函数的定义可知:sinα=$\frac{7\sqrt{2}}{10}$,cosα=$\frac{\sqrt{2}}{10}$,
∴$\frac{1+sin2α}{1+cos2α}$=$\frac{1+2sinαcosα}{2co{s}^{2}α}$=32…6分
(Ⅱ)∵角∠AOB=$\frac{π}{4}$,
∴cos∠COB=cos(α+$\frac{π}{4}$)=cosαcos$\frac{π}{4}$-sinαsin$\frac{π}{4}$=-$\frac{3}{5}$,
∴sin∠COB=sin(α+$\frac{π}{4}$)=sinαcos$\frac{π}{4}$+cosαsin$\frac{π}{4}$=$\frac{4}{5}$,
∴点B(-$\frac{3}{5}$,$\frac{4}{5}$)…12分
点评 本题主要考查了三角函数的定义,二倍角公式,特殊角的三角函数值,两角和的正弦函数、余弦函数公式的综合应用,考查了数形结合思想,属于基础题.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{2}$,0) | B. | ($\frac{π}{4}$,0) | C. | ($\frac{π}{6}$,0) | D. | ($\frac{π}{8}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=Acos(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{6}$)等于( )
函数f(x)=Acos(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{6}$)等于( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,且SE=2EB.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,且SE=2EB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 △ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点.
△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com