
【题目】已知椭圆C ![]() 的离心率为
的离心率为 ![]() ,点
,点 ![]() 在椭圆C上.直线l过点(1,1),且与椭圆C交于A,B两点,线段AB的中点为M. (I)求椭圆C的方程;
在椭圆C上.直线l过点(1,1),且与椭圆C交于A,B两点,线段AB的中点为M. (I)求椭圆C的方程;
(Ⅱ)点O为坐标原点,延长线段OM与椭圆C交于点P,四边形OAPB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
【答案】解:(I)由题意得 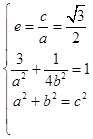 ,解得a2=4,b2=1. 所以椭圆C的方程为
,解得a2=4,b2=1. 所以椭圆C的方程为 ![]() .
.
(Ⅱ)四边形OAPB能为平行四边形,分2种情况讨论:
①当直线l与x轴垂直时,直线l的方程为x=1满足题意;
②当直线l与x轴不垂直时,设直线l:y=kx+m,显然k≠0,m≠0,A(x1 , y1),B(x2 , y2),M(xM , yM).
将y=kx+m代入 ![]() .得(4k2+1)x2+8kmx+4m2﹣4=0,
.得(4k2+1)x2+8kmx+4m2﹣4=0, ![]() .
.
故 ![]() ,
, ![]() .
.
四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分,即 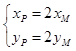 .
.
则 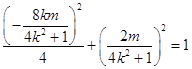 .
.
由直线l:y=kx+m(k≠0,m≠0),过点(1,1),得m=1﹣k.
则 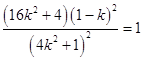 ,
,
则(4k2+1)(8k﹣3)=0.
则 ![]() .满足△>0.
.满足△>0.
所以直线l的方程为 ![]() 时,四边形OAPB为平行四边形.
时,四边形OAPB为平行四边形.
综上所述:直线l的方程为 ![]() 或x=1
或x=1
【解析】(Ⅰ)根据题意,可得 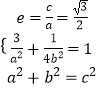 ,解得a2与b2的值,代入椭圆的标准方程即可得答案;(Ⅱ)根据题意,分2种情况讨论,(1)当直线l与x轴垂直时,分析可得直线l的方程为x=1满足题意;(2)当直线l与x轴不垂直时,设直线l为y=kx+m,分析A、B、M的坐标,将y=kx+m代入
,解得a2与b2的值,代入椭圆的标准方程即可得答案;(Ⅱ)根据题意,分2种情况讨论,(1)当直线l与x轴垂直时,分析可得直线l的方程为x=1满足题意;(2)当直线l与x轴不垂直时,设直线l为y=kx+m,分析A、B、M的坐标,将y=kx+m代入 ![]() .得(4k2+1)x2+8kmx+4m2﹣4=0,由根与系数的关系可得M的坐标,进而由四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分可得P的坐标,代入椭圆的标准方程可得
.得(4k2+1)x2+8kmx+4m2﹣4=0,由根与系数的关系可得M的坐标,进而由四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分可得P的坐标,代入椭圆的标准方程可得 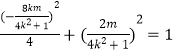 ,进而分析可得
,进而分析可得 ![]() ,解可得k、m的值,即可得答案.
,解可得k、m的值,即可得答案.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,正方形BCDE的边长为a,已知AB= ![]() BC,将△ABE沿边BE折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
BC,将△ABE沿边BE折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述: 
① AB与DE所成角的正切值是 ![]() ;
;
②AB∥CE
③VB﹣ACE体积是 ![]() a3;
a3;
④平面ABC⊥平面ADC.
其中正确的有 . (填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且asinAsinB+bcos2A= ![]() a.
a.
(1)求 ![]() ;
;
(2)若c2=a2+ ![]() b2 , 求角C.
b2 , 求角C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是奇函数,且对于任意x∈R满足f(2﹣x)=f(x),当0<x≤1时,f(x)=lnx+2,则函数y=f(x)在(﹣2,4]上的零点个数是( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
健步走步数(前步) | 16 | 17 | 18 | 19 |
消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅰ)求小王这8天“健步走”步数的平均数;
(Ⅱ)从步数为17千步,18千步,19千步的几天中任选2天,求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.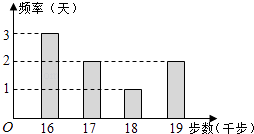
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(4,5cosα),
=(4,5cosα), ![]() =(3,﹣4tanα),α∈(0,
=(3,﹣4tanα),α∈(0, ![]() ),
), ![]() ⊥
⊥ ![]() .
.
(1)求| ![]() ﹣
﹣ ![]() |;
|;
(2)求cos( ![]() +α)﹣sin(α﹣π).
+α)﹣sin(α﹣π).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,已知对任意n∈N* , a1+a2+a3+…+an=3n﹣1,则a12+a22+a32+…+an2等于( )
A.(3n﹣1)2
B.![]()
C.9n﹣1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,﹣4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的三内角A、B、C成等差数列,sinA、sinB、sinC成等比数列,则这个三角形的形状是( )
A.直角三角形
B.钝角三角形
C.等腰直角三角形
D.等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com