练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】2018年2月22日，在韩国平昌冬奥会短道速滑男子500米比赛中，中国选手武大靖以连续打破世界纪录的优异表现，为中国代表队夺得了本届冬奥会的首枚金牌，也创造中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子500米的比赛规则，运动员自出发点出发进入滑行阶段后，每滑行一圈都要经过4个直道与弯道的交接口.已知某男子速滑运动员顺利通过每个交接口的概率均为，摔倒的概率均为.假定运动员只有在摔倒或达到终点时才停止滑行，现在用表示该运动员在滑行最后一圈时在这一圈后已经顺利通过的交接口数.

    (1)求该运动员停止滑行时恰好已顺利通过3个交接口的概率；

    (2)求的分布列及数学期望.

    【答案】(1)；(2)答案见解析.

    【解析】分析：(1)由题意可知.

    (2)的所有可能只为0,1,2,3,4.则，且相互独立.据此可得：，，，，.据此可得分布列，计算相应的数学期望值为.

    详解：(1)由题意可知：.

    (2)的所有可能只为0,1,2,3,4.

    则，且相互独立.

    故，

    ，

    ，

    ，

    .

    从而的分布列为

    0

    1

    2

    3

    4

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．

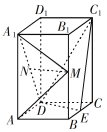
    （1）证明：MN∥平面C1DE；

    （2）求二面角A-MA1-N的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数与的图象上存在关于轴对称的点，则的取值范围是__________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面为矩形，⊥平面，为的中点．

    （Ⅰ）证明：∥平面；

    （Ⅱ）设二面角为60°，=1，=，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆经过点，和直线相切，且圆心在直线上.

    （1）求圆的方程；

    （2）已知直线经过原点,并且被圆截得的弦长为2，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的焦距为，且，圆与轴交于点，，为椭圆上的动点，，面积最大值为.

    （1）求圆与椭圆的方程；

    （2）圆的切线交椭圆于点，，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，平面.

    （1）证明：平面；

    （2）求平面与平面所成二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设平面平面， ， ， ， ， ，

    （1）证明： 平面；

    （2） 求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果存在函数（为常数），使得对函数定义域内任意都有成立，那么称为函数的一个“线性覆盖函数”．给出如下四个结论：

    ①函数存在“线性覆盖函数”；

    ②对于给定的函数，其“线性覆盖函数”可能不存在，也可能有无数个；

    ③为函数的一个“线性覆盖函数”；

    ④若为函数的一个“线性覆盖函数”，则

    其中所有正确结论的序号是___________

    查看答案和解析>>

    同步练习册答案