
【题目】已知圆M:(x+m)2+y2=4n2(m,n>0且m≠n),点N(m,0),P是圆M上的动点,线段PN的垂直平分线交直线PM于点Q,点Q的轨迹为曲线C.
(1)讨论曲线C的形状,并求其方程;
(2)若m=1,且△QMN面积的最大值为![]() .直线l过点N且不垂直于坐标轴,l与曲线C交于A,B,点B关于x轴的对称点为D.求证:直线AD过定点,并求出该定点的坐标.
.直线l过点N且不垂直于坐标轴,l与曲线C交于A,B,点B关于x轴的对称点为D.求证:直线AD过定点,并求出该定点的坐标.
【答案】(1)曲线的形状答案不唯一,见解析,曲线的方程![]() ;(2)见解析,定点(4,0)
;(2)见解析,定点(4,0)
【解析】
(1)当m>n,由题意得QN-QM=2n<2m,此时Q点轨迹为双曲线的左支;当m<n,
QN+QM=2n>2m,此时Q点轨迹为椭圆.根据概念直接求轨迹方程即可得解.
(2)由题意得Q点方程为![]() ,N(1,0),设直线l:x=my+1,A(x1,y1),
,N(1,0),设直线l:x=my+1,A(x1,y1),
B(x2,y2),D(x2,﹣y2),联立方程得![]() ,
,![]() ,表示出直线AD的方程后即可得直线恒过(4,0),即可得证.
,表示出直线AD的方程后即可得直线恒过(4,0),即可得证.
(1)当m>n,即N点在圆M外时,轨迹是双曲线,如图:
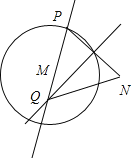
因为QP=QN,则QN-QM=QP-QM=MP=r=2n<MN=2m,
所以点Q的轨迹是以M,N为焦点,以2n为实轴长的双曲线的左支,则Q点轨迹方程为![]() ;
;
当m<n,即N点在圆M内时,轨迹是椭圆,如图:
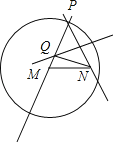
因为QP=QN,则QN+QM=QP+QM=MP=r=2n>MN=2m,所以点Q的轨迹是以M,N为焦点,以2n为长轴长的椭圆,则Q点轨迹方程为![]() ;
;
(2)因为△QMN的面积有最大值,故此时Q点轨迹是椭圆,即Q点所在方程为![]() ,
,
且当Q点为上(下)短轴顶点时△QMN的面积最大,即有![]() 2
2![]() ,
,
解得n2=4,
所以Q点方程为![]() ,N(1,0),设直线l:x=my+1,A(x1,y1),B(x2,y2),D(x2,﹣y2),
,N(1,0),设直线l:x=my+1,A(x1,y1),B(x2,y2),D(x2,﹣y2),
联立![]() ,整理得
,整理得![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,
,
所以直线AD的方程为![]()
![]() ,
,
令y=0,得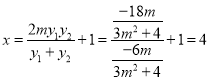 ,
,
则直线AD必过点(4,0),证毕.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】普通高中国家助学金,用于资助家庭困难的在校高中生.在本地,助学金分一等和二等两类,一等助学金每学期1250元,二等助学金每学期750元,并规定:属于农村建档立卡户的学生评一等助学金.某班有10名获得助学金的贫困学生,其中有3名属于农村建档立卡户,这10名学生中有4名获一等助学金,另6名获二等助学金.现从这10名学生中任选3名参加座谈会.
(Ⅰ)若事件A表示“选出的3名同学既有建档立卡户学生,又有非建档立卡户学生”,求A的概率;
(Ⅱ)设X为选出的3名同学一学期获助学金的总金额,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生课外使用手机的情况,某研究学习小组为研究学校学生一个月使用手机的总时间,收集了500名学生2019年12月课余使用手机的总时间(单位:小时)的数据.从中随机抽取了50名学生,将数据进行整理,得到如图所示的频率分布直方图.已知这50人中,恰有2名女生的课余使用手机总时间在![]() 区间,现在从课余使用手总时间在
区间,现在从课余使用手总时间在![]() 样本对应的学生中随机抽取2人,则至少抽到1名女生的概率为( )
样本对应的学生中随机抽取2人,则至少抽到1名女生的概率为( )
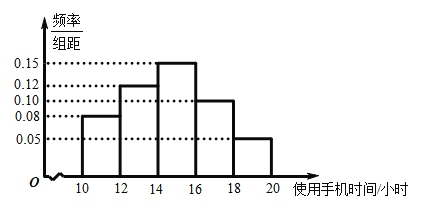
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且
的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且![]() 的面积为1.
的面积为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上位于第一象限内一动点,直线![]() 与
与![]() 轴交于点C,直线
轴交于点C,直线![]() 与
与![]() 轴交于点D,求证:四边形
轴交于点D,求证:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P(3,![]() )是椭圆C:
)是椭圆C:![]() 1
1![]() 上的点,Q是P关于x轴的对称点,椭圆C的离心率为
上的点,Q是P关于x轴的对称点,椭圆C的离心率为![]() .
.
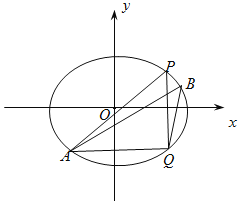
(1)求椭圆C的方程;
(2)A,B是椭圆上位于直线PQ两侧的动点.
①若直线AB的斜率为![]() ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.
②当A、B在运动过程中满足∠APQ=∠BPQ时,问直线AB的斜率是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双11”促销活动中,某商场为了吸引顾客,搞好促销活动,采用“双色球”定折扣的方式促销,即:在红、黄的两个纸箱中分别装有大小完全相同的红、黄球各5个,每种颜色的5个球上标有1,2,3,4,5等5个数字,顾客结账时,先分别从红、黄的两个纸箱中各取一球,按两个球的数字之和为折扣打折,如![]() ,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com