
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,△
,△![]() 是等边三角形,
是等边三角形,![]() 分别为
分别为![]() 的中点.
的中点.
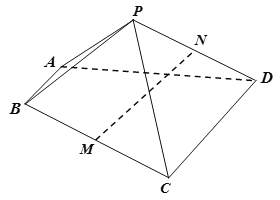
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的大小为
的大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】(1)设曲线![]() 在原点处切线与直线
在原点处切线与直线![]() 垂直,则a=______.
垂直,则a=______.
(2)已知等差数列![]() 中,已知
中,已知![]() ,则
,则![]() =________________.
=________________.
(3)若函数![]() ,则
,则![]() __________.
__________.
(4)曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的图形的面积为__________.
轴围成的图形的面积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() ,
, ![]() :
: ![]() ,和两点
,和两点![]() (0,1),
(0,1),![]() (-1,0),给出如下结论:
(-1,0),给出如下结论:
①不论![]() 为何值时,
为何值时, ![]() 与
与![]() 都互相垂直;
都互相垂直;
②当![]() 变化时,
变化时, ![]() 与
与![]() 分别经过定点A(0,1)和B(-1,0);
分别经过定点A(0,1)和B(-1,0);
③不论![]() 为何值时,
为何值时, ![]() 与
与![]() 都关于直线
都关于直线![]() 对称;
对称;
④如果![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的最大值是1;
的最大值是1;
其中,所有正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的 ![]() 的值为 350,则判断框中可填( )
的值为 350,则判断框中可填( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:
年龄x | 28 | 32 | 38 | 42 | 48 | 52 | 58 | 62 |
收缩压 | 114 | 118 | 122 | 127 | 129 | 135 | 140 | 147 |
其中: ,
,![]() ,
,![]()

![]() 请画出上表数据的散点图;
请画出上表数据的散点图;
![]() 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;![]() 的值精确到
的值精确到![]()
![]() 若规定,一个人的收缩压为标准值的
若规定,一个人的收缩压为标准值的![]() 倍,则为血压正常人群;收缩压为标准值的
倍,则为血压正常人群;收缩压为标准值的![]() 倍,则为轻度高血压人群;收缩压为标准值的
倍,则为轻度高血压人群;收缩压为标准值的![]() 倍,则为中度高血压人群;收缩压为标准值的
倍,则为中度高血压人群;收缩压为标准值的![]() 倍及以上,则为高度高血压人群
倍及以上,则为高度高血压人群![]() 一位收缩压为180mmHg的70岁的老人,属于哪类人群?
一位收缩压为180mmHg的70岁的老人,属于哪类人群?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).

(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三点A(a,0),B(0,b),C(2,2),其中a>0,b>0.
(1)若O是坐标原点,且四边形OACB是平行四边形,试求a,b的值.
(2)若A,B,C三点共线,试求a+b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,动直线
两点,动直线![]() (
(![]() )与
)与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与圆交于
,与圆交于![]() 、
、![]() 两点(点
两点(点![]() 纵坐标大于点
纵坐标大于点![]() 纵坐标).
纵坐标).

(1)若![]() ,点
,点![]() 与点
与点![]() 重合,求点
重合,求点![]() 的坐标;
的坐标;
(2)若![]() ,
,![]() ,求直线
,求直线![]() 将圆分成的劣弧与优弧之比;
将圆分成的劣弧与优弧之比;
(3)若![]() ,设直线
,设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(acosx﹣sinx)![]() (a∈R),且f (
(a∈R),且f (![]() )
)![]() .
.
(1)求a的值;
(2)求f(x)的单调递增区间;
(3)求f(x)在区间[0,![]() ]上的最小值及对应的x的值.
]上的最小值及对应的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com