
【题目】学校对校园进行绿化,移栽香樟和桂花两种大树各2株,若香樟的成活率为![]() ,桂花的成活率为
,桂花的成活率为![]() ,假设每棵树成活与否是相互独立的.求:
,假设每棵树成活与否是相互独立的.求:
(Ⅰ)两种树各成活一株的概率;
(Ⅱ)设ξ表示两种树成活的总株数,求ξ的分布列及数学期望.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】分析:(I)利用![]() 次独立重复试验事件发生
次独立重复试验事件发生![]() 次的概率公式求出“香樟成活一株”和“桂花成活一株”的概率,利用相互独立事件同时发生的概率乘法公式,求出两种树各成活一株的概
次的概率公式求出“香樟成活一株”和“桂花成活一株”的概率,利用相互独立事件同时发生的概率乘法公式,求出两种树各成活一株的概
率;(II) ![]() 的可能取值为
的可能取值为![]() ,,利用互斥事件的概率公式及相互独立事件,同时发生的概率公式,求出随机变量取每一个值的概率,从而可得分布列,进而利用期望公式可得
,,利用互斥事件的概率公式及相互独立事件,同时发生的概率公式,求出随机变量取每一个值的概率,从而可得分布列,进而利用期望公式可得![]() 的数学期望.
的数学期望.
详解: (Ⅰ)记“香樟成活一株”为事件![]() ,“桂花成活一株”为事件
,“桂花成活一株”为事件![]() .
.
则事件“两种树各成活一株”即为事件![]() .
.
![]()
由于事件![]() 与
与![]() 相互独立,因此,
相互独立,因此, ![]() .
.
(Ⅱ)![]() 表示成活的株数,因此
表示成活的株数,因此![]() 可能的取值有0, 1,2, 3,4.
可能的取值有0, 1,2, 3,4.
![]()
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
![]()
![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
因此, ![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)利用绝对值及分段函数知识,将函数![]() 的解析式写成分段函数;
的解析式写成分段函数;
(2)在给出的坐标系中画出![]() 的图象,并根据图象写出函数
的图象,并根据图象写出函数![]() 的单调区间和值域.
的单调区间和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐的单音色旋律,选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.

(Ⅰ) 完成下列2×2列联表;
正误 年龄 | 正确 | 错误 | 合计 |
20~30 | 30 | ||
30~40 | 70 | ||
合计 | 120 |
(Ⅱ)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线过点
,直线过点![]() ,且
,且![]() ,线段
,线段![]() 交圆
交圆![]() 的交点为点
的交点为点![]() ,
,![]() 是
是![]() 关于轴的对称点.
关于轴的对称点.
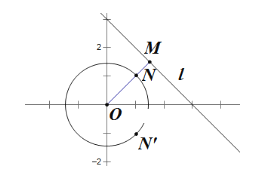
(1)求直线![]() 的方程;
的方程;
(2)已知![]() 是圆
是圆![]() 上不同的两点,且
上不同的两点,且![]() ,试证明直线
,试证明直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )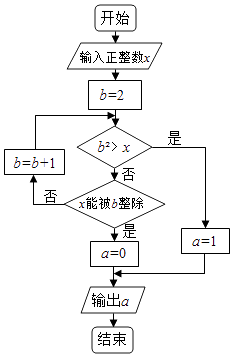
A.0,0
B.1,1
C.0,1
D.1,0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.
(Ⅰ)M为曲线C1上的动点,点P在线段OM上,且满足|OM||OP|=16,求点P的轨迹C2的直角坐标方程;
(Ⅱ)设点A的极坐标为(2, ![]() ),点B在曲线C2上,求△OAB面积的最大值.
),点B在曲线C2上,求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(Ⅰ)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(Ⅱ)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com