
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为( )
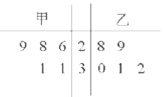
A.①③B.①④C.②③D.②④
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知真命题:“函数![]() 的图象关于点
的图象关于点![]() 成中心对称图形”的等价条件为“函数
成中心对称图形”的等价条件为“函数![]() 是奇函数”.
是奇函数”.
(1)将函数![]() 的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数
的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(2)已知命题:“函数![]() 的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b,使得函数
的图象关于某直线成轴对称图象”的等价条件为“存在实数a和b,使得函数![]() 是偶函数”.断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,
中,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() .
.
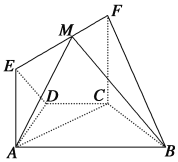
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军在网上经营了一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元/千克.为了增加销量,张军对以上四种干果进行促销,若一次性购买干果的总价达到150元,顾客就少付x(x∈Z)元,每笔订单顾客在网上支付成功后,张军会得到支付款的80%.
①当x=15时,顾客一次性购买松子和腰果各1千克,需要支付_________________元;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销的总价的70%,则x的最大值为___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 具有如下性质:在
具有如下性质:在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)若函数![]() 的值域为
的值域为![]() ,求b的值;
,求b的值;
(2)已知函数![]() ,
,![]() ,求函数
,求函数![]() 的单调区间和值域;
的单调区间和值域;
(3)对于(2)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数c的值.
成立,求实数c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆![]() 相交于不同的两点A,B.
相交于不同的两点A,B.
(1)求线段AB的中点M的轨迹C的方程;
(2)是否存在实数k,使得直线L:y=k(x﹣4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com