
| A. | 13 | B. | 13(lg2)2 | C. | 10 | D. | 10(lg2) |
分析 利用一元二次方程根与系数的关系得到log2a+log2b=-1,log2a•log2b=-3,然后求得lga与lgb的和与积,代入(lg$\frac{a}{b}$)2得答案.
解答 解:∵log2a,log2b是方程x2+x-3=0的两根,
∴log2a+log2b=-1,log2a•log2b=-3.
即$\left\{\begin{array}{l}{lga+lgb=-lg2}\\{lga•lgb=-3l{g}^{2}2}\end{array}\right.$,
∴(lg$\frac{a}{b}$)2=(lga-lgb)2=(lga+lgb)2-4lga•lgb
=(-lg2)2+12lg22=13(lg2)2.
故选:B.
点评 本题考查一元二次方程根与系数的关系,考查了对数的运算性质,是基础的计算题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0° | B. | 60° | C. | 90° | D. | 180° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
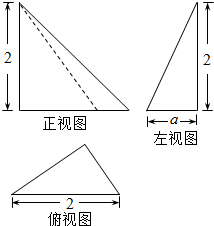
| A. | S是定值,S=8π | B. | S不是定值,有最小值Smin=8π | ||
| C. | S不是定值,有最大值Smax=8π | D. | S不是定值,与a的大小有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com