
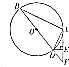
 如图所示,圆O的直径为BD,过圆上一点A作圆O的切线AF交BD的延长线于点F,过点D作DE⊥AF于点E.
如图所示,圆O的直径为BD,过圆上一点A作圆O的切线AF交BD的延长线于点F,过点D作DE⊥AF于点E.分析 (1)推导出∠DAE=∠ABD,∠BAD=90°,∠ABD+∠ADB=90°,∠ADE+∠DAE=90°,由此能证明DA平分∠BDE.
(2)由△BAD∽△AED,得AD=$\sqrt{5}$,从而AE=2,AB=2$\sqrt{5}$,再由△BAF∽△ADF,能求出切线AF的长.
解答 证明:(1)∵AE是⊙O的切线,∴∠DAE=∠ABD,
∵BD是⊙O的直径,∴∠BAD=90°,∠ABD+∠ADB=90°,
又∠ADE+∠DAE=90°,
∴∠ADB=∠ADE,
∴DA平分∠BDE.
解:(2)由(1)知△BAD∽△AED,
∴AD2=DE×BD=1×5=5,∴AD=$\sqrt{5}$,
∴AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=2,AB=$\sqrt{B{D}^{2}-A{D}^{2}}$=2$\sqrt{5}$,
由题意△BAF∽△ADF,
∴DF:AF=AF:BF=AD:AB=1:2,
设AF=x,则${x}^{2}=\frac{x}{2}(5+\frac{x}{2})$,
解得x=$\frac{10}{3}$,
∴切线AF的长为$\frac{10}{3}$.
点评 本题考查DA平分∠BDE的证明,考查切线AF的长的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
“ ”是“不等式
”是“不等式 ”的( )
”的( )
A.充分不必要条件 B.充分必要条件
C.必要不充分条件 D.非充分必要条件
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:选择题
设 ,则“
,则“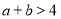 ”是“
”是“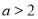 ,且
,且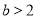 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{53π}{12}$dm3 | B. | $\frac{49π}{12}$dm3 | C. | $\frac{45π}{12}$dm3 | D. | 3πdm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
设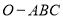 是正三棱锥,
是正三棱锥,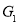 是
是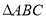 的重心,
的重心,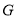 是
是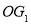 上的一点,且
上的一点,且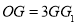 ,若
,若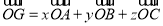 ,则
,则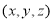 为( )
为( )
A. B.
B.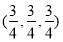
C.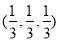 D.
D.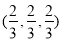
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,底面ABCD为正方形,SD⊥面ABCD,点E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,SD⊥面ABCD,点E,F分别为AB,SC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
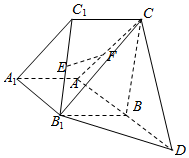 已知三棱柱ABC-A1B1C1中,侧面ABB1A1为正方形,延长AB到D,使得AB=BD,平面AA1C1C⊥平面ABB1A1,A1C1=$\sqrt{2}$AA1,∠C1A1A=$\frac{π}{4}$.
已知三棱柱ABC-A1B1C1中,侧面ABB1A1为正方形,延长AB到D,使得AB=BD,平面AA1C1C⊥平面ABB1A1,A1C1=$\sqrt{2}$AA1,∠C1A1A=$\frac{π}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com