
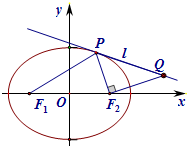
 ��ƽ��ֱ������ϵxoy�У���֪F1��F2�ֱ�����ԲG��
��ƽ��ֱ������ϵxoy�У���֪F1��F2�ֱ�����ԲG��| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| kk1 |
| 1 |
| kk2 |
| y0 |
| x+1 |
| y0 |
| x-1 |
| 1 |
| kk1 |
| 1 |
| kk2 |
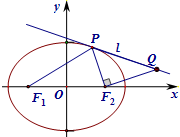 �⣺�����������c=1����
�⣺�����������c=1����| 3 |
| 2a2 |
| 1 |
| b2 |
| 1 |
| 2 |
| x2 |
| 3 |
| y2 |
| 2 |
|
| 3km |
| 2+3k2 |
| 3k |
| m |
|
| x02 |
| 3 |
| y02 |
| 2 |
| 2(3-x02) |
| 3 |
| 2 |
| y0 |
| 2x0 |
| 3y0 |
| 2x0x |
| 3y0 |
| 2 |
| y0 |
| xx0 |
| 3 |
| yy0 |
| 2 |
| y0 |
| x+1 |
| y0 |
| x-1 |
| 1 |
| kk1 |
| 1 |
| kk2 |
| 1 |
| kk1 |
| 1 |
| kk2 |
| 3y0 |
| 2x0 |
| x0+1 |
| y0 |
| x0-1 |
| y0 |
| y0 |
| x0-1 |
| x0-1 |
| y0 |
| x0-1 |
| y0 |
|



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2+2x |
| x2-x |
| x+1 |
| x+2 |
| x2-1 |
| x2+1 |
| 3x-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
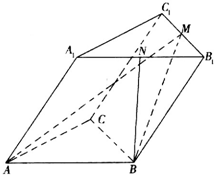 ��ͼ����֪б������ABC-A1B1C1�ĵ������������Σ���M��N�ֱ���B1C1��A1B1���е㣬AA1=AB=BM=2����A1AB=60�㣮
��ͼ����֪б������ABC-A1B1C1�ĵ������������Σ���M��N�ֱ���B1C1��A1B1���е㣬AA1=AB=BM=2����A1AB=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| AB |
| ||
| 2 |
| CD |
| OG |
| OH |
| OP |
| OG |
| OH |
8
| ||
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| 4 |
3
| ||
| 5 |
| a2 |
| 3 |
| PF2 |
| QF2 |
| |PM| |
| |PN| |
| |MH| |
| |HN| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ѧϰ��ͳ��ѧ֪ʶ����λͬѧ�������꼶��1200��ͬѧһ����ѧ���Գɼ����������飬��λͬѧ���ü��������������ȡ100��ѧ���ijɼ���������ѡ����ѧ�ɼ��Ƴ�����ͳ�Ʊ����豾�ο��Ե������������Ϊ90�֣��ŵ�����ͷ�130�֣����ҿ��Գɼ�������[85��90����ѧ��ͨ������Ŭ���ܴﵽ�������������
��ѧϰ��ͳ��ѧ֪ʶ����λͬѧ�������꼶��1200��ͬѧһ����ѧ���Գɼ����������飬��λͬѧ���ü��������������ȡ100��ѧ���ijɼ���������ѡ����ѧ�ɼ��Ƴ�����ͳ�Ʊ����豾�ο��Ե������������Ϊ90�֣��ŵ�����ͷ�130�֣����ҿ��Գɼ�������[85��90����ѧ��ͨ������Ŭ���ܴﵽ�������������| ������ | [70��80�� | [80��90�� | [90��100�� | [100��110�� | [110��120�� | [120��130�� | [130��140�� | [140��150�� |
| ���� | 9 | 6 | 12 | 18 | 21 | 16 | 12 | 6 |
| Ƶ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| �� |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| �� |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
A��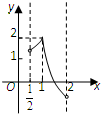 |
B�� |
C�� |
D��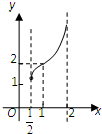 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com