练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若对任意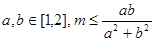恒成立，则m的最大值是        

     

    【答案】

    【解析】

    试题分析：因为,令z=. 作出表示的平面区域，可知,所以的最大值为，所以的最小值为,所以,所以m的最大值是.

    考点：简单的线性规划，斜率的几何意义，的单调性与最值.

    点评：本小题看似是一个不等式恒成立问题，实质是一个与线性规划结合的一个函数最值题，关键是把式子,然后令z=.根据,结合z的几何意义可求出z的范围，然后求出的最小值为,问题得解。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：湖南省澧县一中、岳阳县一中2012届高三11月联考数学文科试题 题型：022

    若对任意恒成立，则m的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年吉林省高考复习质量检测数学理卷 题型：解答题

    请考生在第（22）、（23）、（24）三题中任选一题做答，如果多做，则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。

    （本小题满分10分）选修4—1：几何证明选讲

    如图，⊙O是的外接圆，D是的中点，BD交AC于E。

       （I）求证：CD2=DE·DB。

       （II）若O到AC的距离为1，求⊙O的半径。

    （本小题满分10分）

    选修4—4：作标系与参数方程

    已知直线的参数方程为（t为参数），曲线C的极坐标方程为，以极点为原点，极轴为x轴正半轴建立直角坐标系，M点坐标为（0，2），直线与曲线C交于A，B两点。

       （I）写出直线的普通方程与曲线C的直角坐标方程；

       （II）线段MA，MB长度分别记|MA|，|MB|，求|MA|·|MB|的值。

    （本小题满分10分）选修4—5：不等式选讲

    设函数

       （I）画出函数的图象；

       （II）若对任意恒成立，求a-b的最大值。

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年吉林省高考复习质量检测数学理卷 题型：解答题

    请考生在第（22）、（23）、（24）三题中任选一题做答，如果多做，则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。

    （本小题满分10分）选修4—1：几何证明选讲

    如图，⊙O是的外接圆，D是的中点，BD交AC于E。

       （I）求证：CD2=DE·DB。

       （II）若O到AC的距离为1，求⊙O的半径。

    （本小题满分10分）

    选修4—4：作标系与参数方程

    已知直线的参数方程为（t为参数），曲线C的极坐标方程为，以极点为原点，极轴为x轴正半轴建立直角坐标系，M点坐标为（0，2），直线与曲线C交于A，B两点。

       （I）写出直线的普通方程与曲线C的直角坐标方程；

       （II）线段MA，MB长度分别记|MA|，|MB|，求|MA|·|MB|的值。

    （本小题满分10分）选修4—5：不等式选讲

    设函数

       （I）画出函数的图象；

       （II）若对任意恒成立，求a-b的最大值。

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年天津市蓟县一中高三（上）第一次月考数学试卷（理科）（解析版） 题型：填空题

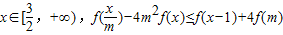    （1）设函数f（x）=x2-1，对任意恒成立，则实数m的取值范围是    ．
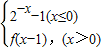    （2）函数f（x）=，若方程f（x）=x+a恰有两个不等的实根，则a的取值范围是    ．

    查看答案和解析>>

    同步练习册答案