试题分析:由平面向量的夹角公式得,
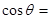

=
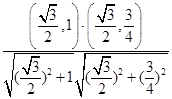
=

点评:简单题,注意应用

。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
如图,在
△ABC中,设
BC,CA, AB的长度分别为
a,b,c,证明:
a2=b2+c2-2bccosA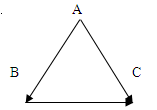
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知
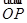
=
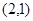
,
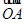
=
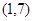
,
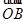
=
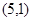
,设
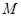
是直线
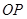
上一点,
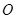
是坐标原点
(1)求使
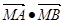
取最小值时的
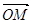
;
(2)对(1)中的点
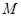
,求
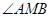
的余弦值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
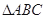
内接于以
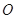
为圆心,
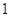
为半径的圆,且
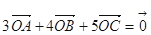
,
(1)求数量积
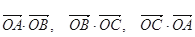
;(6分)
(2)求
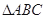
的面积. (6分)
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
平面向量
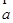
与
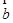
的夹角为
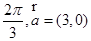
,
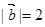
,则
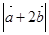
=( )
A.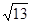 | B.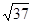 | C.7 | D.3 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知点
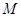
为等边三角形
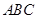
的中心,
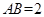
,直线
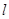
过点
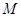
交边
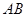
于点
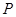
,交边

于
点
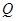
,则
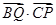
的最大值为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
如图,在梯形ABCD中,AD∥BC,则
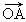
+
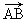
-
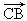
等于( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
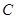
为线段
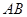
上一点,
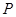
为直线
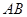
外一点,满
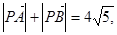
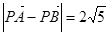
,
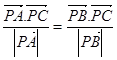
,
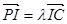
,
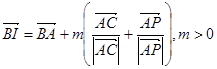
则
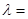
( )
| A.1 | B.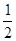 | C.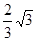 | D.2 |
查看答案和解析>>
