
(Ⅰ)方程f(x)=0有实根;
(Ⅱ)-2<![]() <-1;
<-1;
(Ⅲ)设x1,x2是方程f(x)=0的两个实根,则![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.
证明:(Ⅰ)若a=0,则b=-c,f(0)·f(1)=c(3a+2b+c)=-c2≤0与已知矛盾,∴a≠0,方程3ax2+2bx+c=0的判别式Δ=4(b2-3ac),由条件a+b+c=0,消去b得Δ=4(a2+c2-ac)=4[(a-![]() c)2+
c)2+![]() c2]>0.
c2]>0.
故方程f(x)=0有实根.
(Ⅱ)由f(0)·f(1)>0得,c(3a+2b+c)>0,由条件a+b+c=0消去C得(a+b)(2a+b)<0,因a2>0,∴(![]() +1)(
+1)(![]() +2)<0.
+2)<0.
故-2<![]() <-1.
<-1.
(Ⅲ)由条件知:x1+x2=-![]() ,x1-x2=
,x1-x2=![]() =-
=-![]() .
.
所以(x1-x2)2=(x1+x2)2-4x1x2=![]() (
(![]() +
+![]() )2+
)2+![]() ,
,
因为-2<![]() <-1,所以
<-1,所以![]() ≤(x1-x2)2<
≤(x1-x2)2<![]() ,
,
故![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.


科目:高中数学 来源:2012年人教B版高中数学必修5 3.3 一元二次不等式及其解法练习卷(解析版) 题型:解答题
设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)>0,f(1)>0
求证:(1)a>0,-2<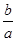 <-1
<-1
(2)函数f(x)在(0,1)内有零点。
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)=3ax2+2bx+c,若a+b+c=0.f(0)>0,f(1)>0,
求证: (Ⅰ)a>0且-2<![]() <-1;
<-1;
(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)a>0且-2<![]() <-1;
<-1;
(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)a>0且-2<![]() <-1;
<-1;
(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)方程f(x)=0有实根;
(Ⅱ)-2<![]() <-1;
<-1;
(Ⅲ)设x1,x2是方程f(x)=0的两个实根,则![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com