
ЁОЬтФПЁПФГЭтТєЦНЬЈЮЊЬсИпЭтТєХфЫЭаЇТЪЃЌеыЖдЭтТєХфЫЭвЕЮёЬсГіСЫСНжжаТЕФХфЫЭЗНАИЃЌЮЊБШНЯСНжжХфЫЭЗНАИЕФаЇТЪЃЌЙВбЁШЁ50УћЭтТєЦяЪжЃЌВЂНЋЫћУЧЫцЛњЗжГЩСНзщЃЌУПзщ25ШЫЃЌЕквЛзщЦяЪжгУМзХфЫЭЗНАИЃЌЕкЖўзщЦяЪжгУввХфЫЭЗНАИ.ИљОнЦяЪждкЯрЭЌЪБМфФкЭъГЩХфЫЭЖЉЕЅЕФЪ§СПЃЈЕЅЮЛЃКЕЅЃЉЛцжЦСЫШчЯТОЅвЖЭМЃК
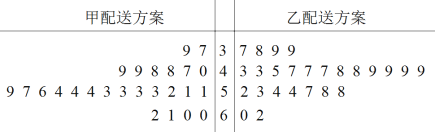
ЃЈ1ЃЉИљОнОЅвЖЭМЃЌЧѓИїзщФк25ЮЛЦяЪжЭъГЩЖЉЕЅЪ§ЕФжаЮЛЪ§ЃЌвбжЊгУМзХфЫЭЗНАИЕФ25ЮЛЦяЪжЭъГЩЖЉЕЅЪ§ЕФЦНОљЪ§ЮЊ52ЃЌНсКЯжаЮЛЪ§гыЦНОљЪ§ХаЖЯФФжжХфЫЭЗНАИЕФаЇТЪИќИпЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЩшЫљга50УћЦяЪждкЯрЭЌЪБМфФкЭъГЩЖЉЕЅЪ§ЕФЦНОљЪ§![]() ЃЌНЋЭъГЩЖЉЕЅЪ§ГЌЙ§
ЃЌНЋЭъГЩЖЉЕЅЪ§ГЌЙ§![]() МЧЮЊЁАгХауЁБЃЌВЛГЌЙ§
МЧЮЊЁАгХауЁБЃЌВЛГЌЙ§![]() МЧЮЊЁАвЛАуЁБЃЌШЛКѓНЋЦяЪжЕФЖдгІШЫЪ§ЬюШыЯТУцСаСЊБэЃЛ
МЧЮЊЁАвЛАуЁБЃЌШЛКѓНЋЦяЪжЕФЖдгІШЫЪ§ЬюШыЯТУцСаСЊБэЃЛ
гХау | вЛАу | |
МзХфЫЭЗНАИ | ||
ввХфЫЭЗНАИ |
ЃЈ3ЃЉИљОнЃЈ2ЃЉжаЕФСаСЊБэЃЌХаЖЯФмЗёга![]() ЕФАбЮеШЯЮЊСНжжХфЫЭЗНАИЕФаЇТЪгаВювь.
ЕФАбЮеШЯЮЊСНжжХфЫЭЗНАИЕФаЇТЪгаВювь.
ИНЃК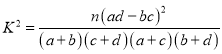 ЃЌЦфжа
ЃЌЦфжа![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
ЁОД№АИЁПЃЈ1ЃЉМзжаЮЛЪ§ЮЊ53ЃЛввжаЮЛЪ§ЮЊ49ЃЛМзХфЫЭЗНАИЕФаЇТЪИќИпЃЌЯъМћНтЮіЃЈ2ЃЉЬюБэМћНтЮіЃЛЃЈ3ЃЉга![]() ЕФАбЮеШЯЮЊСНжжХфЫЭЗНАИЕФаЇТЪгаВювь
ЕФАбЮеШЯЮЊСНжжХфЫЭЗНАИЕФаЇТЪгаВювь
ЁОНтЮіЁП
ЃЈ1ЃЉОЅвЖЭМЭъШЋЗДгГЫљгаЕФдЪМЪ§ОнЃЌгЩОЅвЖЭМжБНгЕУМзжаЮЛЪ§53ЃЌввжаЮЛЪ§49
ЃЈ2ЃЉЧѓГіЦНОљЪ§![]() гЩОЅвЖЭМЪ§ОнжБНгЬюШы
гЩОЅвЖЭМЪ§ОнжБНгЬюШы![]() СаСЊБэЃЌ
СаСЊБэЃЌ
ЃЈ3ЃЉДњШыЙЋЪНЃЌМЦЫуГі![]() ЕФжЕЃЌгыЖРСЂадМьбщХаЖЯБэБШНЯзїГіХаЖЯ.
ЕФжЕЃЌгыЖРСЂадМьбщХаЖЯБэБШНЯзїГіХаЖЯ.
НтЃКЃЈ1ЃЉгУМзХфЫЭЗНАИЕФЦяЪжЭъГЩЭтТєЖЉЕЅЪ§ЕФжаЮЛЪ§ЮЊ53ЃЌ
гУввХфЫЭЗНАИЕФЦяЪжЭъГЩЭтТєЖЉЕЅЪ§ЕФжаЮЛЪ§ЮЊ49ЃЌ
вђЮЊгУввХфЫЭЗНАИЕФЦяЪжЭъГЩЭтТєЖЉЕЅЪ§ЕФЦНОљЪ§ЮЊ![]() Чв
Чв![]() ЃЌ
ЃЌ
ЫљвдЃЌМзХфЫЭЗНАИЕФаЇТЪИќИп.
ЃЈ2ЃЉгЩОЅвЖЭМжЊ![]() .
.
СаСЊБэШчЯТЃК
гХау | вЛАу | |
МзХфЫЭЗНАИ | 17 | 8 |
ввХфЫЭЗНАИ | 9 | 16 |
ЃЈ3ЃЉвђЮЊ![]() ЃЌ
ЃЌ
Ыљвдга![]() ЕФАбЮеШЯЮЊСНжжХфЫЭЗНАИЕФаЇТЪгаВювь.
ЕФАбЮеШЯЮЊСНжжХфЫЭЗНАИЕФаЇТЪгаВювь.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ТњзуЦцЪ§Яю
ТњзуЦцЪ§Яю![]() ГЩЕШВюЃЌЙЋВюЮЊ
ГЩЕШВюЃЌЙЋВюЮЊ![]() ЃЌХМЪ§Яю
ЃЌХМЪ§Яю![]() ГЩЕШБШЃЌЙЋБШЮЊ
ГЩЕШБШЃЌЙЋБШЮЊ![]() ЃЌЧвЪ§Са
ЃЌЧвЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
![]() Шє
Шє![]() ЃЌ
ЃЌ![]() .
.
ЂйЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЂкШє![]() ЃЌЧѓе§ећЪ§
ЃЌЧѓе§ећЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
![]() Шє
Шє![]() ЃЌ
ЃЌ![]() ЃЌЖдШЮвтИјЖЈЕФ
ЃЌЖдШЮвтИјЖЈЕФ![]() ЃЌЪЧЗёДцдкЪЕЪ§
ЃЌЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЖдШЮвт
ЖдШЮвт![]() КуГЩСЂЃПШєДцдкЃЌЧѓГі
КуГЩСЂЃПШєДцдкЃЌЧѓГі![]() ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() дк
дк![]() ДІЕФЧаЯпЗНГЬЃК
ДІЕФЧаЯпЗНГЬЃК
ЃЈ2ЃЉвбжЊЪЕЪ§![]() ЪБЃЌЧѓжЄЃККЏЪ§
ЪБЃЌЧѓжЄЃККЏЪ§![]() ЕФЭМЯѓгыжБЯп
ЕФЭМЯѓгыжБЯп![]() ЃК
ЃК![]() га3ИіНЛЕуЃЎ
га3ИіНЛЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЯТЮЊМђЛЏЕФМЦЛЎЩњг§ФЃаЭЃКУПИіМвЭЅдЪаэЩњФаКЂзюЖрвЛИіЃЌМДФГвЛЬЅШєЮЊФаКЂЃЌдђВЛФмдйЩњЯТвЛЬЅЃЌЖјХЎКЂПЩвдЖрИі.ЮЊЗНБуЦ№МћЃЌДЫДІдМЖЈУПИіМвЭЅзюЖрПЩЩњг§3ИіаЁКЂЃЌМДШєЕквЛЬЅЛђЧАСНЬЅЮЊХЎКЂЃЌдђМЬајЩњЃЌЕЋШєЕкШ§ЬЅЛЙЪЧХЎКЂЃЌдђВЛФмдйЩњСЫ.ЩшУПвЛЬЅЩњФаЩњХЎЕШПЩФмЃЌЧвИїДЮЩњг§ЯрЛЅЖРСЂ.вРОнУПИіМвЭЅзюЖрЩњг§вЛИіФаКЂЕФеўВпвдМАЮвУЧЖдЩњг§ХЎКЂЕФдМЖЈЃЌСю![]() ЮЊФГвЛМвЭЅЫљЩњЕФХЎКЂЪ§ЃЌ
ЮЊФГвЛМвЭЅЫљЩњЕФХЎКЂЪ§ЃЌ![]() ЮЊДЫМвЭЅЫљЩњЕФФаКЂЪ§.
ЮЊДЫМвЭЅЫљЩњЕФФаКЂЪ§.
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() ЕФЗжВМСаЃЌВЂБШНЯЫќУЧЪ§бЇЦкЭћЕФДѓаЁЃЛ
ЕФЗжВМСаЃЌВЂБШНЯЫќУЧЪ§бЇЦкЭћЕФДѓаЁЃЛ
ЃЈ2ЃЉЧѓИХТЪ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЮЊ
ЮЊ![]() ЕФЗНВю.
ЕФЗНВю.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫСЫНтдЫЖЏНЁЩэМѕЗЪЕФаЇЙћЃЌФГНЁЩэЗПЕїВщСЫ20УћЗЪХжепЃЌНЁЩэжЎЧАЫћУЧЕФЬхжи(ЕЅЮЛЃК![]() )ЧщПіШчжљаЮЭМ1ЫљЪОЃЌОЙ§ЫФИідТЕФНЁЩэКѓЃЌЫћУЧЕФЬхжиЧщПіШчжљаЮЭМ2ЫљЪО.ЖдБШНЁЩэЧАКѓЃЌЙигкет20УћЗЪХжепЃЌЯТУцНсТле§ШЗЕФЪЧЃЈ ЃЉ
)ЧщПіШчжљаЮЭМ1ЫљЪОЃЌОЙ§ЫФИідТЕФНЁЩэКѓЃЌЫћУЧЕФЬхжиЧщПіШчжљаЮЭМ2ЫљЪО.ЖдБШНЁЩэЧАКѓЃЌЙигкет20УћЗЪХжепЃЌЯТУцНсТле§ШЗЕФЪЧЃЈ ЃЉ
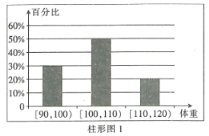
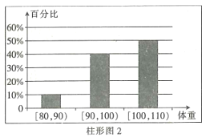
A.ЫћУЧНЁЩэКѓЃЌЬхжидкЧјМф![]() ФкЕФШЫЪ§діМгСЫ2Иі
ФкЕФШЫЪ§діМгСЫ2Иі
B.ЫћУЧНЁЩэКѓЃЌЬхжидкЧјМф![]() ФкЕФШЫЪ§УЛгаИФБф
ФкЕФШЫЪ§УЛгаИФБф
C.вђЮЊЬхжидк![]() ФкЫљеМБШР§УЛгаЗЂЩњБфЛЏЃЌЫљвдЫЕУїНЁЩэЖдЬхжиУЛгаШЮКЮгАЯь
ФкЫљеМБШР§УЛгаЗЂЩњБфЛЏЃЌЫљвдЫЕУїНЁЩэЖдЬхжиУЛгаШЮКЮгАЯь
D.ЫћУЧНЁЩэКѓЃЌдРДЬхжидкЧјМф![]() ФкЕФЗЪХжепЬхжиЖМгаМѕЩй
ФкЕФЗЪХжепЬхжиЖМгаМѕЩй
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЬжТл![]() ЕФМЋжЕЕуЕФИіЪ§ЃЛ
ЕФМЋжЕЕуЕФИіЪ§ЃЛ
ЃЈ2ЃЉЩшКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЧњЯп
ЮЊЧњЯп![]() ЩЯШЮвтСНИіВЛЭЌЕФЕуЃЌЩшжБЯп
ЩЯШЮвтСНИіВЛЭЌЕФЕуЃЌЩшжБЯп![]() ЕФаБТЪЮЊ
ЕФаБТЪЮЊ![]() ЃЌШє
ЃЌШє![]() КуГЩСЂЃЌЧѓ
КуГЩСЂЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНЬхABCDЉA1B1C1D1жаЃЌMЃЌNЃЌPЗжБ№ЪЧC1D1ЃЌBCЃЌA1D1ЕФжаЕуЃЌгаЯТСаЫФИіНсТлЃК
ЂйAPгыCMЪЧвьУцжБЯпЃЛЂкAPЃЌCMЃЌDD1ЯрНЛгквЛЕуЃЛЂлMNЁЮBD1ЃЛ
ЂмMNЁЮЦНУцBB1D1DЃЎ
ЦфжаЫљгае§ШЗНсТлЕФБрКХЪЧЃЈЁЁЁЁЃЉ

A.ЂйЂмB.ЂкЂмC.ЂйЂмD.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЮЊЦНУцЩЯвЛЕуЃЌ
ЮЊЦНУцЩЯвЛЕуЃЌ![]() ЮЊжБЯп
ЮЊжБЯп![]() ЃК
ЃК![]() ЩЯШЮвтвЛЕуЃЌЙ§Еу
ЩЯШЮвтвЛЕуЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЕФДЙЯп
ЕФДЙЯп![]() ЃЌЩшЯпЖЮ
ЃЌЩшЯпЖЮ![]() ЕФжаДЙЯпгыжБЯп
ЕФжаДЙЯпгыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌМЧЕу
ЃЌМЧЕу![]() ЕФЙьМЃЮЊ
ЕФЙьМЃЮЊ![]() .
.
ЃЈ1ЃЉЧѓЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() зїЛЅЯрДЙжБЕФжБЯп
зїЛЅЯрДЙжБЕФжБЯп![]() гы
гы![]() ЃЌЦфжажБЯп
ЃЌЦфжажБЯп![]() гыЙьМЃ
гыЙьМЃ![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыЙьМЃ
гыЙьМЃ![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() КЭ
КЭ![]() ЕФжаЕуЃЌЧѓ
ЕФжаЕуЃЌЧѓ![]() ЕФУцЛ§ЕФзюаЁжЕ.
ЕФУцЛ§ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁАМваЃСЌаФЃЌСЂЕТЪїШЫЁЊЁЊжиЮТАЎЙњЙЪЪТЃЌКыбяАЎЙњжївхОЋЩёЩчЛсПЮЬУЁБЛюЖЏжаЃЌЭѕРЯЪІзщНЈСЫвЛИіЮЂаХШКЃЌШКЕФГЩдБгЩбЇЩњЁЂМвГЄЁЂРЯЪІКЭНВНтдБЙВЭЌзщГЩ.вбжЊИУЮЂаХШКжаФабЇЩњШЫЪ§ЖргкХЎЩњШЫЪ§ЃЌХЎбЇЩњШЫЪ§ЖргкМвГЄШЫЪ§ЃЌМвГЄШЫЪ§ЖргкНЬЪІШЫЪ§ЃЌНЬЪІШЫЪ§ЖргкНВНтдБШЫЪ§ЃЌНВНтдБШЫЪ§ЕФСНБЖЖргкФаЩњШЫЪ§.ШєАбет5РрШЫШКЕФШЫЪ§зїЮЊвЛзщЪ§ОнЃЌЕБИУЮЂаХШКзмШЫЪ§ШЁзюаЁжЕЪБЃЌетзщЪ§ОнЕФжаЮЛЪ§ЪЧЃЈ ЃЉ
A.5B.6C.7D.8
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com