
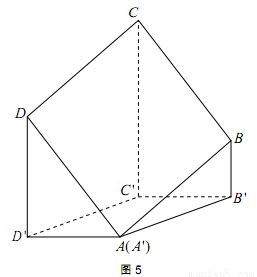
如图 5,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形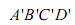 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.
(1)证明AD'//平面BB'C'C,并指出四边形AB'C'D’的形状;
(2)如果四边形中AB'C'D’中, ,正方形的边长为
,正方形的边长为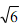 ,
,
求平面ABCD与平面AB'C'D’所成的锐二面角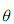 的余弦值.
的余弦值.
见解析.
【解析】第一问是涉及到线面平行的判定,以及四边形的形状问题的证明。
第二问关于二面角的求解,可以利用射影面积公式法,也可以利用法向量的夹角公式来解,通过合理的建立直角坐标系,表示向量,然后求解斜率的夹角,利用互为补角的关系求解得到二面角的大小。
解:(2)依题意,在Rt△ABB’中,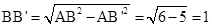 ,
,
在Rt△ADD’中,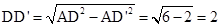 ,
,
所以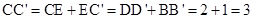 .………………8分
.………………8分
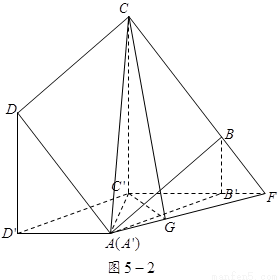
连结AC,AC’,如图5-2,在Rt△ACC’中, .
.
所以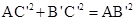 ,故
,故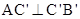 .……10分
.……10分
(法1)延长CB,C’B’相交于点F,
则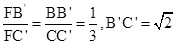 ,所以
,所以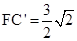 .
.
连结AF,则AF是平面ABCD与平面AB’C’D
的交线.
在平面AB’C’D
内作C’G,垂足为G,
连结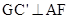 .
.
因为 平面AB’C’D,
平面AB’C’D,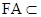 平面AB’C’D,所以
平面AB’C’D,所以 AF.
AF.
从而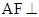 平面CC’G,
平面CC’G,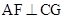 .
.
所以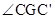 是平面ABCD与平面AB’C’D所成的一个锐二面角. …………12分
是平面ABCD与平面AB’C’D所成的一个锐二面角. …………12分
在Rt△AC’F中,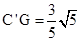 ,
,
在Rt△CC’G中, .
.
所以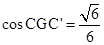 ,
,
即平面ABCD与平面AB'C'D’所成的锐二面角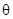 的余弦值为
的余弦值为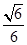 .………14分
.………14分

(法2)以c’为原点,c’a为x轴,c’b’为y轴,c’c为z轴,
建立空间直角坐标系(如图5-3),
则平面AB’C’D的一个法向量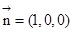 .
.
设平面ABCD的一个法向量为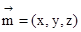 ,
,
因为
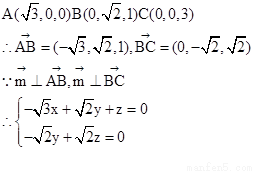
取z=1,则y=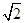 ,x=
,x=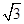 ,所以平面ABCD的一个法向量为
,所以平面ABCD的一个法向量为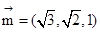 .
.
(注:法向量不唯一,可以是与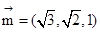 共线的任一非零向量)……………12分
共线的任一非零向量)……………12分
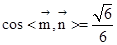 .
.
所以平面ABCD与平面AB’C’D所成的锐二面角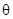 的余弦值为
的余弦值为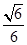 . …………………14分
. …………………14分
(法3)由题意,正方形ABCD在水平面上的正投影是四边形AB’C’D,
所以平面ABCD与平面AB’C’D,所成的锐二面角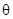 的余弦值
的余弦值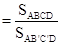 . …………12分
. …………12分
所以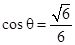 ,
,
所以平面ABCD与平面AB’C’D所成的锐二面角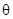 的余弦值为
的余弦值为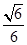 . …………………14分
. …………………14分


科目:高中数学 来源: 题型:
 (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.| 2 |
| 5 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2010年山东省高一下学期期末考试数学卷 题型:选择题
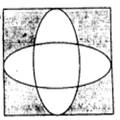
如图,已知正方形的面积为10,向正方形
内随机地撒200颗黄豆,数得落在阴影外
的黄豆数为114颗,以此实验数据为依据,
可以估计出阴影部分的面积约为( )
A.5.3 B.4.3
C.4.7 D.5.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com