
 .对于A=(a1,a2,…,an),B=(b1,b2,…,bn)∈Sn,定义
.对于A=(a1,a2,…,an),B=(b1,b2,…,bn)∈Sn,定义 ;λ(a1,a2,…,an)=(λa1,λa2,…,λan)(λ∈R);A与B之间的距离为
;λ(a1,a2,…,an)=(λa1,λa2,…,λan)(λ∈R);A与B之间的距离为 .
. ,则d(A,B)+d(B,C)=d(A,C);
,则d(A,B)+d(B,C)=d(A,C);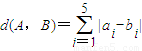 ,求得 d(A,B)的值.
,求得 d(A,B)的值.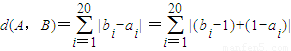
 ,等号成立的条件为ai=1,或bi=1,从而得到 d(A,B)≤26,由此可得结论.
,等号成立的条件为ai=1,或bi=1,从而得到 d(A,B)≤26,由此可得结论.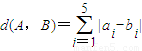 ,
,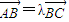 ,
,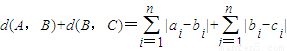
 =
=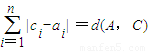 .
.
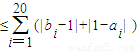
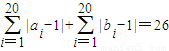 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知集合![]() ,对于它的非空子集A,将A中的每个元素k,都乘以
,对于它的非空子集A,将A中的每个元素k,都乘以![]() 再求和,(如A = {1,3,6},可求和得到
再求和,(如A = {1,3,6},可求和得到![]() ),则对M的所有非空子集,这些和的总和是________________.
),则对M的所有非空子集,这些和的总和是________________.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市徐汇区高三第一学期期中试卷数学 题型:填空题
若X是一个集合,τ是一个以X的某些子集为元素的集合,且满足:①X属于τ, 属于τ;
属于τ;
②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑.已知集合X ={a,b,c},对于下面给出的四个集合τ:
①τ={ ,{a}, {c}, {a, b, c}}; ②τ={
,{a}, {c}, {a, b, c}}; ②τ={ ,{b}, {c}, {b, c}, {a, b, c}};
,{b}, {c}, {b, c}, {a, b, c}};
③τ={ ,{a}, {a, b}, {a, c}}; ④τ={
,{a}, {a, b}, {a, c}}; ④τ={ ,{a, c}, {b, c}, {c}, {a, b, c}}.
,{a, c}, {b, c}, {c}, {a, b, c}}.
其中是集合X上的拓扑的集合τ的序号是_________________
查看答案和解析>>
科目:高中数学 来源:西南师大附中2010届高三第五次月考(数学理)试题 题型:填空题
已知集合 ,对于它的非空子集A,将A中的每个元素k,都乘以
,对于它的非空子集A,将A中的每个元素k,都乘以 再求和,(如A = {1,3,6},可求和得到
再求和,(如A = {1,3,6},可求和得到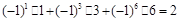 ),则对M的所有非空子集,这些和的总和是________________.
),则对M的所有非空子集,这些和的总和是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com