已知集合A={x|x2-6x+8<0},B={x|(x-a)•(x-3a)<0}.
(1)若A∪B=B,求实数a的取值范围;
(2)若A∩B={x|3<x<4},求实数a的值.
解:A={x|2<x<4},
(1)∵A∪B=B,∴A⊆B,
a>0时,B={x|a<x<3a},
∴
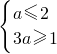
,解得

≤a≤2
a<0时,B={x|3a<x<a},显然A?B;
a=0时,B=Φ,显然不符合条件
∴

≤a≤2时,A∪B=B
(2)要满足A∩B={x|3<x<4},由(1)知,a>0且a=3时成立.
∵此时B={x|3<x<9},A∩B={x|3<x<4},
故所求的a值为3.
分析:(1)先解不等式x
2-6x+8<0,得集合A,(1)由于不等式(x-a)•(x-3a)<0的解集与a的取值有关,故讨论a的范围,得集合B,再利用数轴得满足条件的a的不等式,解得a的范围;
(2)由(1)知,若A∩B={x|3<x<4},则a>0且a=3时成立,从而得a的值
点评:本题主要考查了一元二次不等式的解法,集合间的关系,集合的运算,分类讨论的思想方法,转化化归的思想方法

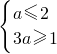 ,解得
,解得 ≤a≤2
≤a≤2 ≤a≤2时,A∪B=B
≤a≤2时,A∪B=B

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案